由 Filmlight 公司的色彩科学专家理查德·柯克(Richard Kirk)撰写的色彩科学白皮书《颜色:感知与测量》(Colour: Sense & Measurement)第四章(翻译初稿)
译者:Horace Lu
原书下载地址
- 视亮度(brightness)、色相(hue)和饱和度(saturation)
- 孟塞尔颜色图册(The Munsell Colour Atlas)
- 孟塞尔颜色系统的明度(Value),色相(Hue)和彩度(Chroma)
- 含混不清的颜色术语
- Yxy 色彩空间
- Yu’v’ 色彩空间
- 白光
- 孟塞尔参考基准(The Munsell Benchmark)
- 显示器伽马校正
- 场景(scene)与显示(display)
- 伽马测试图
- CIE L*a* b* (CIELAB)
- CIE 2006 标准中的 tRGB
- 从 tRGB 衍生的 tLAB
- 恰可察觉差(Just Noticeable Differendce, JND)
- Delta E(△E)
- 主波长(dominant wavelength)
- 均匀色彩空间
在上一章中,我们讨论了颜色的测量方法,介绍了标准观察者空间,这些空间能够判断两次光谱测量是否在视觉上相匹配。在本章中,我们将进一步探讨基于这些标准观察者所生成的色彩空间,这些空间不仅反映了颜色本身的特性,还确保了数值上的等距变化对应颜色外观的均匀变化(similar steps in the values correspond to similar steps in the appearance)。在深入讨论之前,为了了解背景,我们先介绍一些简单的亮度-色度(luma-chroma)术语,并讲解一些色彩空间,以及我们对 黑色 和 白色 这两个术语的理解。随后我们将探讨孟塞尔颜色图册(Munsell Colour Atlas)中的反射颜色的特性。
视亮度(brightness)、色相(hue)和饱和度(saturation)
完美的黑色吸收所有光线而不反射光线,完美的白色则反射所有光线而不吸收光线。虽然我们无法实现完美的黑色和白色,但我们能制造出反射率低于 1% 以及高于 99% 的材料。通过半调(halftone)技术,我们可以在这两个极端之间创造出各种灰度。
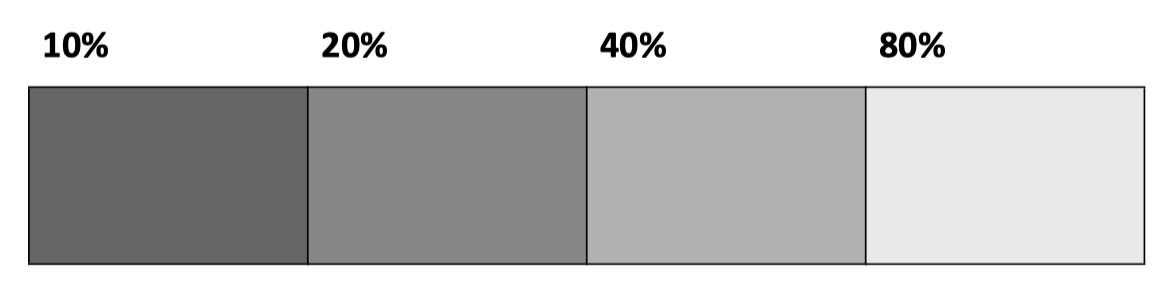
在上图中,每个色块反射的光量是前一个色块的两倍。虽然我不能保证你在图中看到的实际色块完全符合这个规律,但应该不会相差太多。任何两个色块之间的视觉对比度看起来都大致相同,这个现象可以通过上一章提到的颜色恒常性来解释。试想一下,如果光照水平增加一倍,你会感觉到光线变亮了,但你的眼睛会适应这种变化,使得物体看起来与之前无异。在这里,尽管白色的周围环境(surround)会产生一定影响,但色块间的对比度依然保持一致。可以看出,光线水平的等比变化表现为 视亮度(brightness) 的等距变化。这个规则并非绝对,因为如果光线太暗,我们就无法分辨出亮度的等距变化;如果光线太亮,我们会感到炫目,也无法准确判断亮度变化。然而,如果我们要求某人挑选不同灰度的色块,排列形成视亮度(brightness)的等距变化,他们的选择大致上会遵循这一规律。
那么,对于颜色是否有类似规律呢?在上一章中我们讨论了光亮度(luminance)的概念。如果以每秒 5 次或更高的频率在两种颜色之间快速切换时无法察觉闪烁现象,就说明这两种颜色具有相同的光亮度(luminance)。需要注意的是,此处的光亮度(luminance)和我们所讨论的视亮度(brightness)不一定相对应。然而,如果我们要求某人挑选一个灰色色块,使其视亮度(brightness)与某种指定颜色相匹配,他们选择的结果也往往是相似的。
对于彩色和灰色而言,它们的光亮度(luminance)比例是否看起来也保持一致呢?答案是肯定的。这个论点与之前基本相同,只不过这里使用的是彩色光而非白色光。因此,我们现在似乎得到了一个适用于所有颜色的、具有均匀视觉步长的亮度临时标度(provisional scale for brightness)。
随便选择一种颜色,同时找到一种具有相同视亮度(brightness)的灰色。现在,让我们把这种灰色与选定的颜色混合起来。下图是一个混合黑色和红色的例子,在色块上方标注了红色所占的百分比。
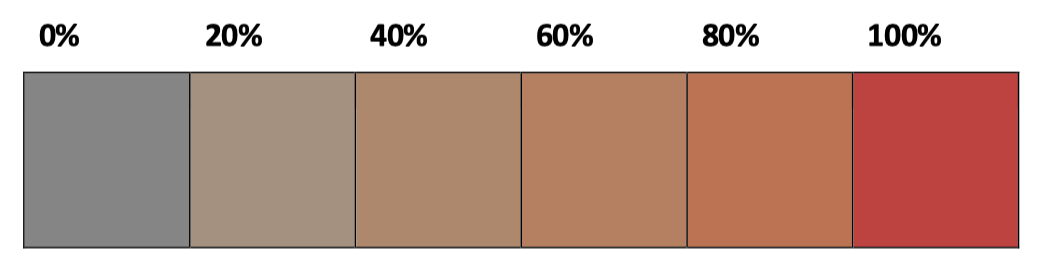
我们得到了一组从灰色过渡到红色的步长。同时,有一个视亮度(brightness)参数从黑色逐渐变化为白色。这个新引入的参数通常称为 饱和度(saturation)。饱和度在几个步长的对比度似乎相当一致。虽然我们不能像视亮度(brightness)那样简单地生成饱和度的均匀步长,但在色块边界处的对比度看起来相当均匀。如果我们要求某人将彩色色卡按照饱和度的均匀步长等距排列,他们的做法大致也是这样。
理论上,饱和度可以是负值。每种颜色都有一个具有相同视亮度(brightness)的对立色(opposite colour),二者混合后可以产生中性色。例如,红色的对立色是青色。如果混合青色和红色,就可以创造出一组更长的色块序列,序列的右半部分会与上图看起来很接近,但中性色不一定位于序列的中间位置。
在第三章的“三色近似理论”部分有一张插图,显示了具有相同光亮度(luminance)的 530 纳米绿色和 460 纳米蓝色所混合出的三角形。在图中,中性灰位于中心位置,而饱和色则围绕在三角形的边缘。尽管我们的颜色范围可能与该图不同,但颜色的总体布局应该是相似的。这里缺少的第三个参数称为 色相(hue),通常以色相角(hue angle)表示,其中红色位于 0 °。按照惯例,我们不采用“负饱和度”这一概念,而是通过将色相角调整 180 度来确保饱和度是正值。
虽然我们可以明确给出任何指定颜色的对立色,但准确定义一组感知步长均匀的色相却没那么简单。不过,如果要求某人选择视亮度(brightness)相同的色卡,并将它们按相同饱和度排列成同心圆,然后沿着圆周以均匀的色相角步长进行排序,这种方法似乎是可行且合理的。
在实践中,最后一个“合理要求”可能并不实际可行。我们可以把颜色分配到一系列具有相同饱和度的圆环上,并尝试在每个圆环中按色相对比度均匀排列颜色,但这样做无法保证其他圈环中的色相也能对齐。因此,在一个三维空间中可能无法找到一个完全满足感知均匀性的坐标系。不过我们可以尽量接近这个目标:首先选出一个最大、最饱和、且包含全部色相的圆环,使其颜色排列看起来协调,然后再把其他色相与这个大圆环对齐。
基于以上概略论证可以推测,所有颜色都应该存在一个感知上均匀的视亮度(brightness)标度,以及另外两个称为色相(hue)和饱和度(saturation)的维度。理论上,如果足够多的人拿着彩色色卡,将其按照感知上的等距步长进行排列,那么应当有可能就视亮度(brightness)、色相(hue)、明度(value)这三个维度的的感知均匀步长集合达成一致。
世界上第一套标准色卡是由阿尔伯特·亨利·孟塞尔(Albert Henry Munsell,1858-1918)制作的。一个多世纪以来,人们一直在努力实现这一目标。让我们来看看他们取得了怎样的进展。
孟塞尔颜色图册(The Munsell Colour Atlas)
1905 年,阿尔伯特·亨利·孟塞尔发布了《颜色符号》(A Colour Notation)一书,描述了一个与我们上文所述原理类似的色彩坐标系统。1913 年,他进一步出版了《颜色立体图鉴》(The Atlas of the Colour Solid),其中包含精确的颜色样例。后来他又推出了附带可拆卸色卡的《孟塞尔色彩大全》(The Munsell Book of Colour),这本书出版至今仍在印刷。一个多世纪以来,书中的色彩集合不断扩充,但其底层系统仍保持不变。
孟塞尔颜色系统有三个参数:明度(Value,即 lightness)、色相(Hue)、彩度 (Chroma,即饱和度 saturation)。《孟塞尔颜色图册》(The Munsell Colour Atlas)根据人眼在正常日光条件下判定的均匀间隔,将彩色色卡按照色相、明度、彩度三个参数进行规律排列。在孟塞尔最初的实验中,“日光”可能采用了现已废弃的 CIE 标准光源 C,其色温约为 6700 K。如果我们在 6500 K 照明下观察《孟塞尔色彩大全》中的色卡,可能会得到与孟塞尔原始实验接近的结果。此外,《色彩大全》在 D50 光照下也呈现出一致性,而 D50 是反射介质观察灯箱(reflection media viewing booths)的标准光源。上述两种白色光源涵盖了大多数电影、电视及印刷品的观看条件。
孟塞尔颜色系统在感知均匀性方面相比于 OSA-UCS 或 CIECAM02 等色彩空间可能稍逊一筹。它是一套随时间不断更新颜色的色卡集,虽然并未指定具体的照明光源,但在 D50 至 D65 之间的白光照明下具有相对一致的色彩表现。在系统中,彩度(Chroma,hue)轴的表示方法有些特殊,然而它的基础十分简单实用:色卡展示了颜色的等距变化,是因为研究人员不断试验,直至达到视觉上的和谐统一。近期新推出的一些色彩更饱和的色卡可能得益于新的视觉模型的辅助设计,但最终它们仍需通过真人观察验证。因此,在我们探索基于三刺激值 XYZ 或 LMS 的感知均匀色彩空间时,我们将使用《孟塞尔色彩大全》作为参考基准(benchmark)进行比较。如果在这些色彩空间中,颜色点的分布看起来与孟塞尔颜色系统相似,那么就意味着它们的工作机制是有效的。
孟塞尔颜色系统的明度(Value),色相(Hue)和彩度(Chroma)
在本章开头,我们提到了三个描述颜色的参数——视亮度(brightness)、色相(hue)和饱和度(saturation)。其中,视亮度(brightness)可能会呈现出感知均匀的等比例步长变化,而色相(hue)和饱和度(saturation)的步长则可能需要依赖人眼的直观判断。以下是孟塞尔颜色系统的示意图。
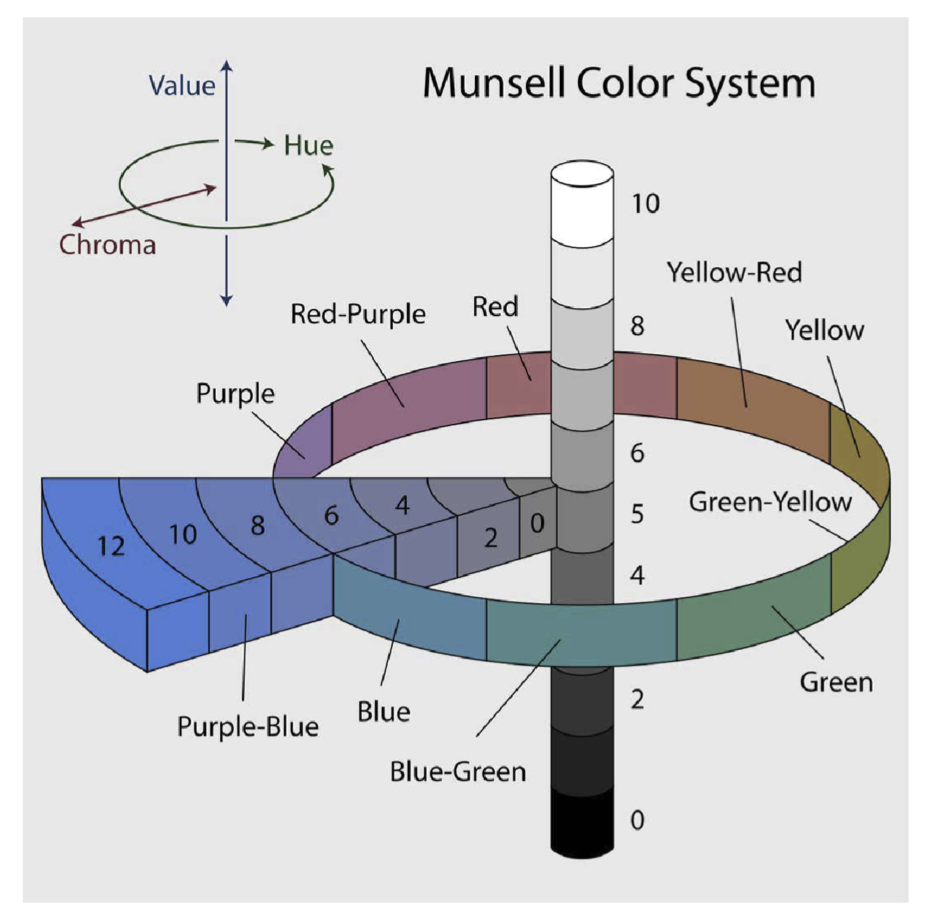
垂直坐标称为明度(Value),其范围从 0(黑色)延伸至 10(白色)。在其他系统中,这一坐标可能被称为 视亮度(brightness)、明度(lightness),或简称为 值(value)。理论上,改变一个颜色的视亮度(brightness)很简单:只需将其颜色光谱中的所有值等比例放大,即可在颜色保持不变的基础上增加每个色彩成分的量。
圆环上的坐标称为 色相(Hue),在其他系统中称为 色相(hue) 或 色相角(hue angle)。色相角的取值范围为 0 到 360 度。孟塞尔的色相(Hue)分为十个配有相应名称的颜色带,每个颜色带包含编号从 0 到 9 的十种颜色,其中 5 位于中心位置。一个颜色带中的 0 实际上对应于前一个颜色带的 10,如果存在 10,则对应下一个颜色带的 0。在《孟塞尔色彩大全》中包含了 40 种色相,以 2.5 为步长进行了区分。
最后一个坐标是彩度(Chroma),是从中性轴向外测量的半径。图中展示了一段彩度(Chroma)值的变化区间,从 0(中性,无彩色)到 12(鲜艳的蓝紫色)。彩度(Chroma)的范围依赖于明度(Value)和色相(Hue)。在其他系统中,这一坐标称为 饱和度(saturation) 或 彩色强度(chromatic intensity)。术语“饱和度”的最初提出者及原因并不明确,但现在已被广泛使用。彩度从 0(即灰色,无彩色)开始逐渐向外增加,饱和度逐渐增强,直到达到完全饱和状态,无法再进一步增强色彩。
含混不清的颜色术语
有时人们会把饱和的颜色称为“明亮的(bright)颜色”。建议不要使用这个术语,在别人使用时也要注意辨析。亥姆霍兹-科尔劳施效应(Helmholtz-Kohlrausch effect)表明,极其明亮(bright)且饱和(saturated)的颜色似乎有一种“发光”感,因此饱和度(saturation)与视亮度(apparent brightness)确实存在一定的感知重叠。我们在第七章中还会再次讨论亥姆霍兹-科尔劳施效应。在此之前,请与我一起将“明亮(bright)”用作“昏暗(dim)”的反义词,而不是“饱和(saturated)”的同义词。
视亮度(brightness)、色相(hue)、饱和度(saturation) 这三个术语,常被用来描述我们所看到的颜色。它们在用户界面设计中应用广泛,但在数字成像领域很少使用,因为它们难以进行插值运算。色相轴是一个环形结构:360 度 与 0.0 度表示相同的色相。当穿过中性轴时,饱和度不会变为负值,而是保持正值,而色相则会发生 180 度的反转。在图像颜色处理中,通常更容易采用 XYZ、RGB 或 LMS 等三维笛卡尔坐标系。
亮度(Brightness)这个词的含义可能依赖于上下文的具体背景。如果你询问一个显示器有多亮(how bright)时,答案通常会以尼特(nits)给出。尽管大多数关于亮度的感知测量(perceptual measurement of brightness)都是基于光亮度(luminance)的值,但尼特本身并非感知度量标准:在 1000 尼特的显示器上几乎察觉不到 1 尼特的变化,但在 0.1 尼特的环境中,1 尼特的微小变化却足以使阴影细节消失不见。
还有另一种常见用法:彩度(chroma)通常用来描述除了光亮度(luminance)之外的所有颜色特性。在接下来我们即将了解的 Yxy 和 Yu’v’ 色彩空间中,我们可能会称 Y 为光亮度(luminance),而 xy 或 u’v’ 表示 彩度(chroma)。孟塞尔系统特别使用 彩度(Chroma) 或 彩色强度(Chromatic Intensity) 来指代饱和度。在本书中,我将使用首字母“c”小写的“chroma”作为一般彩度的术语,而首字母“C”大写的“’Chroma”特指孟塞尔系统中的彩度坐标轴。为了区分,本文档中非孟塞尔系统的彩度轴(chroma axis)将以 粗体 表示。
Yxy 色彩空间
Yxy 色彩空间是最简单的光亮度-色度(luminance-chrominance)空间。它通过以下公式从 CIE 1931 XYZ 色彩空间派生而来:
其中,Y 代表光亮度(luminance),以尼特为单位,而 x 和 y 是两个无量纲的坐标数值,用来描述颜色。其逆变换形式如下:
在 xy 空间中,颜色具有线性混合的特性:若在 xy 平面上连接两个点,这条直线上的任意点都可以通过线段两端的色光经过线性混合得到。然而,这一空间在感知上并不均匀:在蓝紫色区域,即使是很小的 x 和 y 值变化也会更容易察觉,而在绿色区域,同样的变化则不那么明显。
下图展示了 CIE xy 空间中,波长从 400 纳米到 700 纳米的颜色分布。
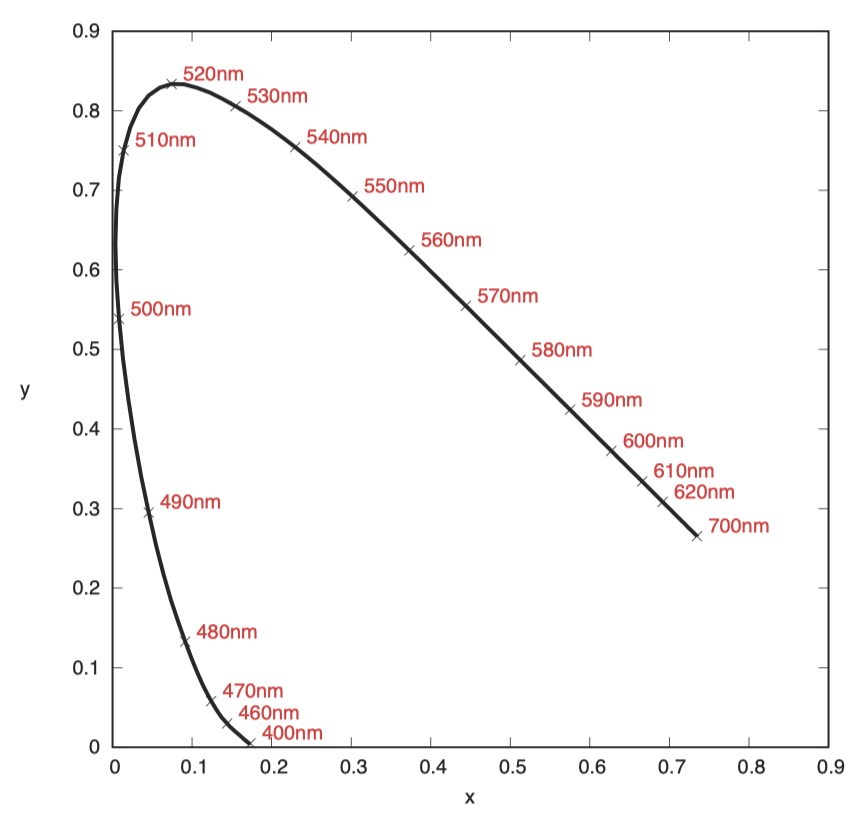
Yu’v’ 色彩空间
Yu’v’ 色彩空间是一种均匀的光亮度-色度(luminance-chrominance)空间,它通过以下公式从 XYZ 空间派生而来:
其中,Y 仍然是光亮度(luminance),以尼特为单位;u’ 和 v’ 是两个无量纲的坐标数值,用于描述颜色。其逆变换形式如下:
Yu’v’ 空间对蓝紫色区域进行了拉伸处理,而对绿色角落进行了压缩。虽不尽完美,但视觉均匀性相较于 xy 空间有所改善。u’v’ 空间同样支持颜色的线性混合。
值得一提的是,在 u’v’ 空间之前还存在过一个 uv 空间,但仅在短短一年内就被 Yu’v’ 所取代。因此,当前提及的 Yuv 通常是指 Yu’v’ 。尽管如此,在 Yuv 空间中有一种构造方法,可以针对给定的近似白(near-white)找到最接近的热源白(thermal white),这种方法仍在使用中。然而,在 uv 空间中应用这种构造方法并无明显优势,因为使用计算机可以轻松在 u’v’ 空间中找到最近点。我自己的计算结果总是与文献中的略有区别,这就是其中的原因。
下图展示了 CIE u’v’ 空间中,波长从 400 纳米到 700 纳米的颜色分布。
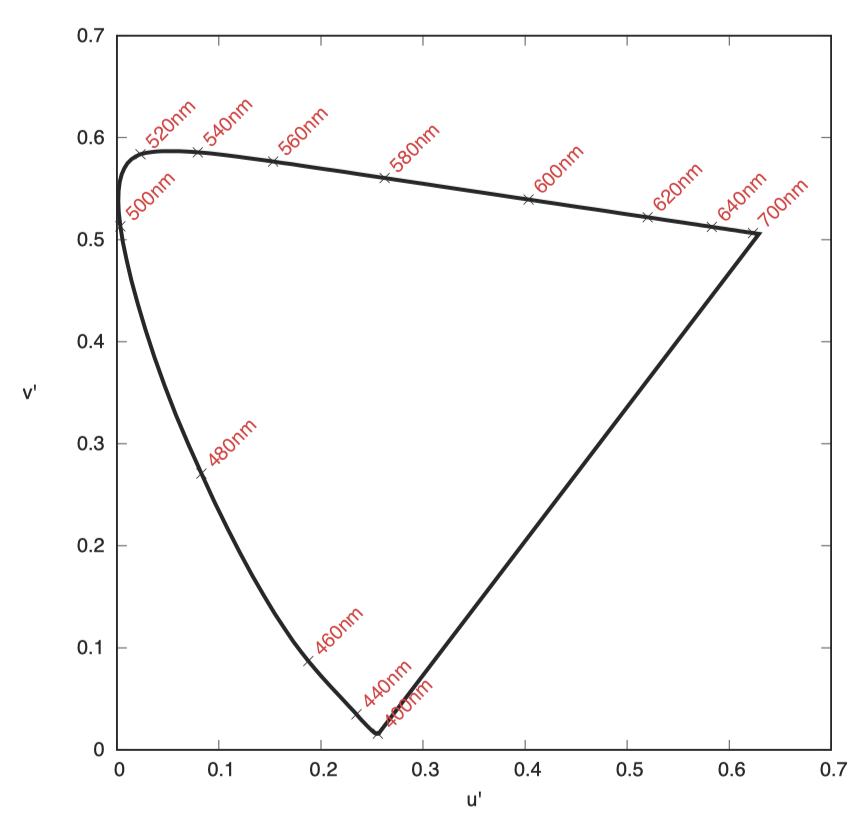
白光
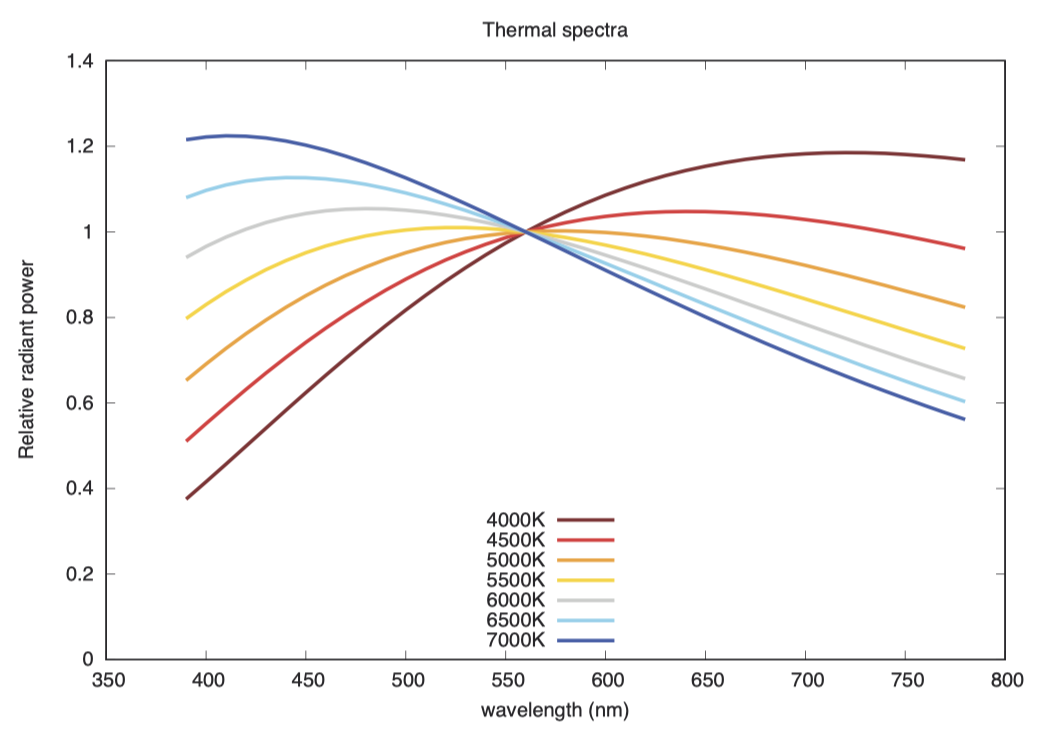
高温物体(hot body)会产生白光,光谱通常取决于物体的形状、材质和温度。如果我们有一个内部温度均匀的大空腔,并通过小孔采集其中的光线以避免显著干扰空腔中的辐射平衡,那么此时腔体发光的光谱仅取决于其本身的温度。这类光谱被称为黑体光谱(blackbody spectra)、热线谱(thermal spectra)、白炽光谱(incandescent spectra)或普朗克光谱(Planckian spectra)。
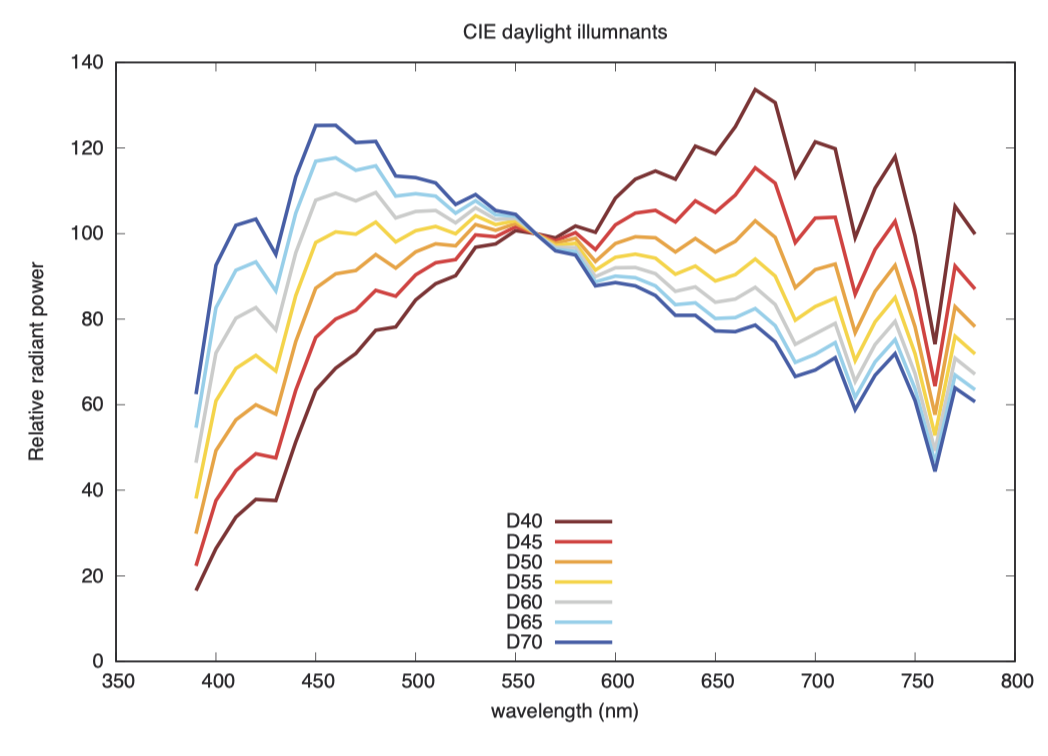
CIE 标准日光光源是基于日光光谱的测量结果建立的。日光光谱在多种条件下测量,并简化为一个平均光谱,以及另外两种可组合成一系列光谱的光谱函数。这些光谱通常根据其近似色温进行命名。例如,D65 是一种近似色温为 6500K 的日光光源(Daylight illuminant)。
然而,市面上并不存在完全符合 CIE 光谱的光源,因为它们的光谱分布过于复杂,在人造灯具中很难复制。这种 CIE 日光模拟光源只存在于理论计算的理想状态下。当人们将荧光管描述为“D65”时,通常指的是该荧光管的颜色与 D65 相匹配,这一匹配是通过标准观察者模型来评估的。
CIE 日光光源并非一定遵循热轨迹(thermal locus)[1]。虽然它们非常接近,但仍有微小的偏差,如下图。
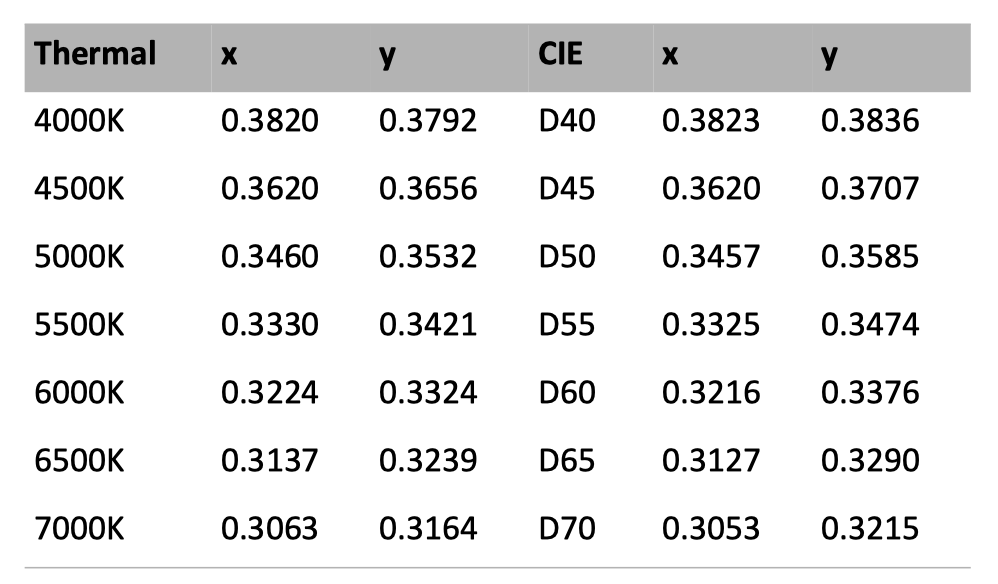
以下是一系列光源的色温值,其中哪一个才是“真正的”白色呢?实际上,包括以下光源在内,许多热源都能给人以白色的视觉感受。
关键在于,无论是热源的光谱值还是 CIE 日光光源的白色光谱值,它们都紧贴着一条共同的曲线。如果偏离这条曲线,光线就会呈现出粉色或绿色,显得非常不自然。实际上,所有自然光源和大多数人造光源的光谱特性都符合黑体曲线(blackbody curve),这正是我们所习惯且喜欢的视觉效果。
在进行光源模拟时,我通常选择使用黑体曲线,因为它们具有平滑且规律良好(well-behaved)的特点。在采用 CIE 日光光源进行模拟时,也能得到几乎相同的结果。然而,像荧光灯或 LED 灯这样的实际光源,虽然看起来是白色的,但其光谱中可能存在峰值,这些峰值会影响我们看到的颜色。
孟塞尔参考基准(The Munsell Benchmark)
《孟塞尔色彩大全》提供了一套按照明度(Value)、色相(Hue)和彩度(Chroma,即彩色纯度或饱和度)的感知均匀步长来排序的色卡。虽然这些参数不能直接测量,但它们的含义在色彩科学中已经得到了广泛的共识。假设我们在 5000K 到 6700K 范围内的光源照明下对孟塞尔色卡进行测量,在此范围内的孟塞尔色卡在视觉上是感知均匀的。如果把这些色卡放在其他感知均匀色彩空间里绘制其位置,那么它们的明度层级(Value layers)、色相角(Hue angles)和彩度圆环(Chroma circles)也应该与孟塞尔空间一致。
在此,我们展示了从孟塞尔空间明度(Value) 4 级色卡中测量出的一些 Yxy 值。理论上,这些颜色应该共享相同的光亮度(luminance) Y 值。
这些数据是通过光谱仪(spectrometer)从光滑材料上测得的实验值。虽然其分布并非理想状态下的圆形,但我们能看到一些扭曲的椭圆形状。通过想象,我们或许可以识别出具有相同色相的辐射线状点群。
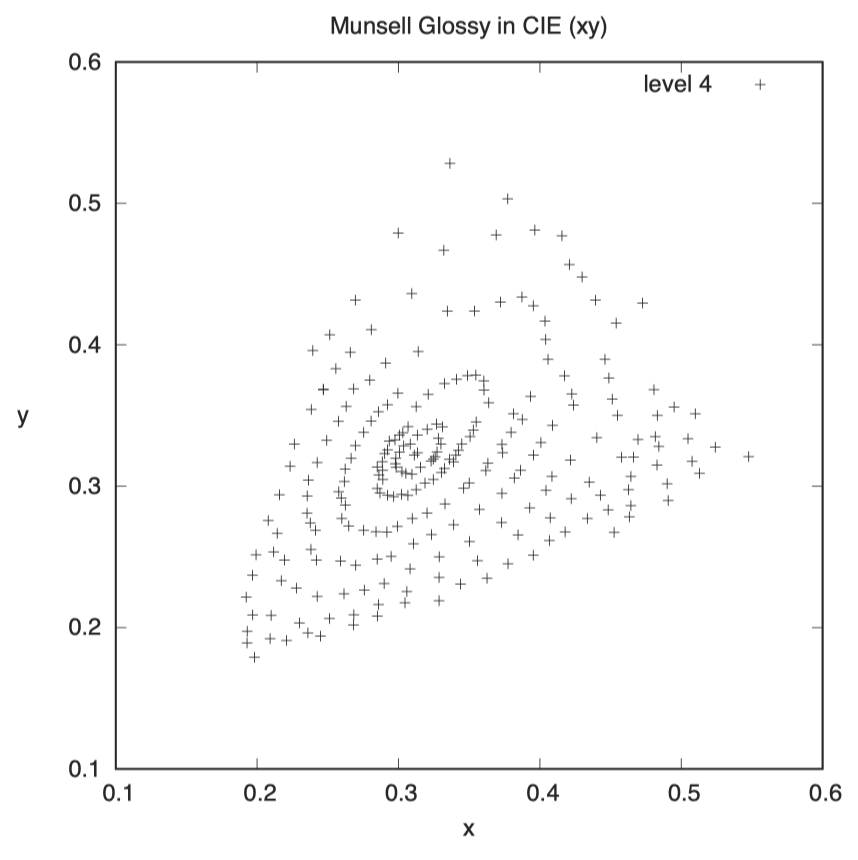
接下来,我们用同样的方法测量这些色卡在 Yu’v’ 空间的表现:
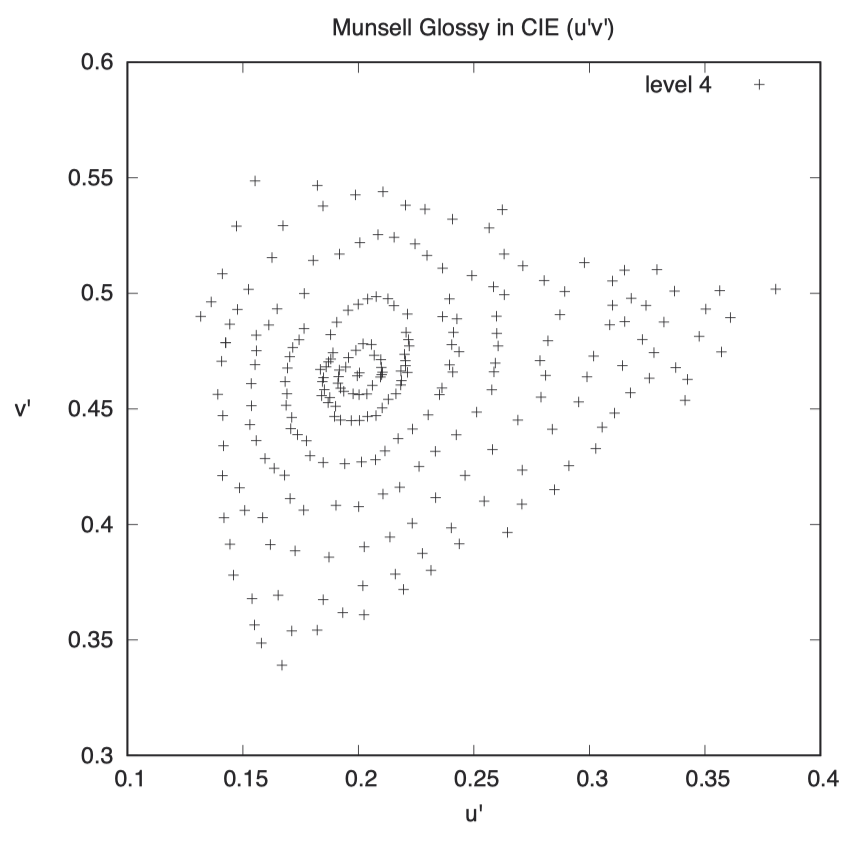
Yu’v’ 空间虽然结构简单,但其选择的颜色轴相较于 Yxy 空间能提供更为均匀的颜色对比度。可以看到,这里的椭圆比在 Yxy 坐标系中更接近圆形了。
我采用了 6500K 的黑体光谱进行模拟照明,然而 Yu’v’ 色彩空间并不预设任何特定的光源信息。可能存在其他光源能够进一步改善模拟结果,当然也有一些光源可能导致结果变差。
最后,我们来关注 Y 值。对于 Yxy 和 Yu’v’ 空间而言,Y 值是相同的,因此可以用一张图代表两者的情况:
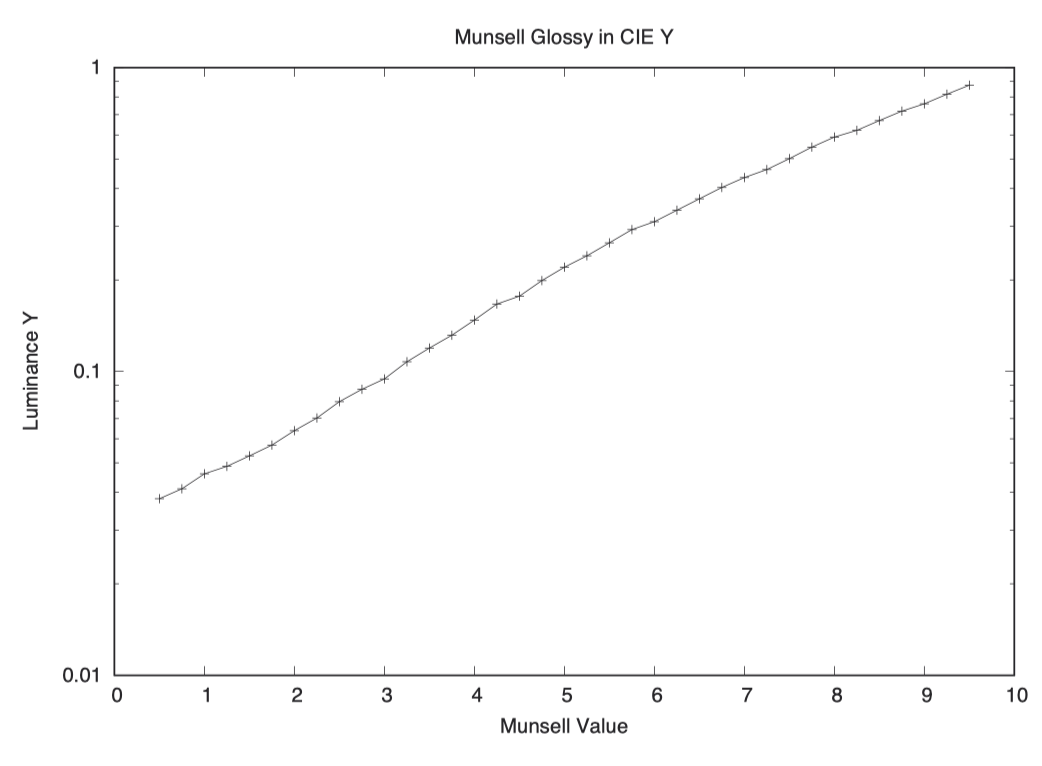
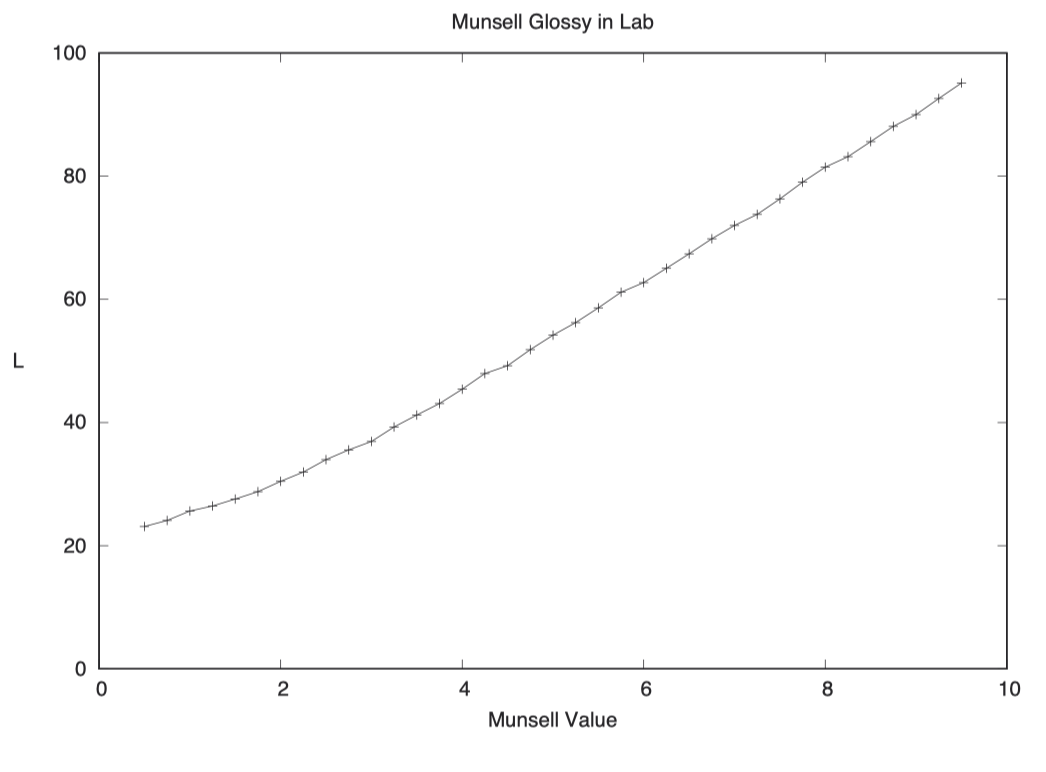
孟塞尔明度(Value)的等距变化对应着相近的视觉对比度。我们针对一组中性色卡,将其孟塞尔明度(Value)与对应的反射 Y 值(reflection Y)绘制在上图中,在 Y 轴采用对数刻度。结果显示几乎是一条直线,这意味着孟塞尔明度(Value)的等距变化可以产生相近的 Y 值斜率,至少在孟塞尔色卡的有限范围内是这样。
为了展示我们对明度(lightness)感知的非线性特质,让我们尝试通过肉眼比较孟塞尔明度(Value)与线性亮度水平(linear light level)之间的差异。虽然这种比较方式存在不确定性,但我希望读者不论是通过印刷品还是电子显示设备观看,都能大致看出我所观察到的结果。下图列出了 9 块模拟的孟塞尔色块,其明度(Value)值从 1 到 9,置于黑色背景上。在其下方是一组亮度水平均匀递增的相似色块。在这两组色块中,第一块和最后一块的灰色是上下相同的。
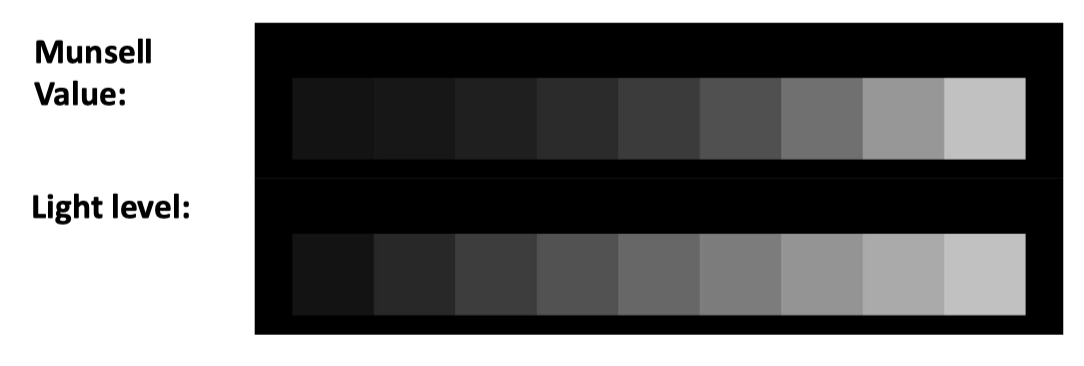
在我的显示器与环境光条件下,在孟塞尔色块中,左侧 1 和 2 色块之间的对比度很难分辨出来,但其他色块之间的对比度看起来则相当接近。在下方的亮度水平色块中,对比度主要集中在左侧,第 2 个色块几乎与中间的孟塞尔色块 5 几乎没有区别。
显示器伽马校正
显示技术常常依赖于一种简单的幂律色调函数(power law tone function):
其中希腊字母γ(伽马)代表显示器的伽马值。
在视频领域,伽马值通常设定为 2.4。虽然它并不像对数尺度那样在相同对比度下提供相等的增量,但它同样能够在暗部区域拉伸对比度,并且能够平滑地降至零点,而对数尺度则永远无法达到绝对的零。
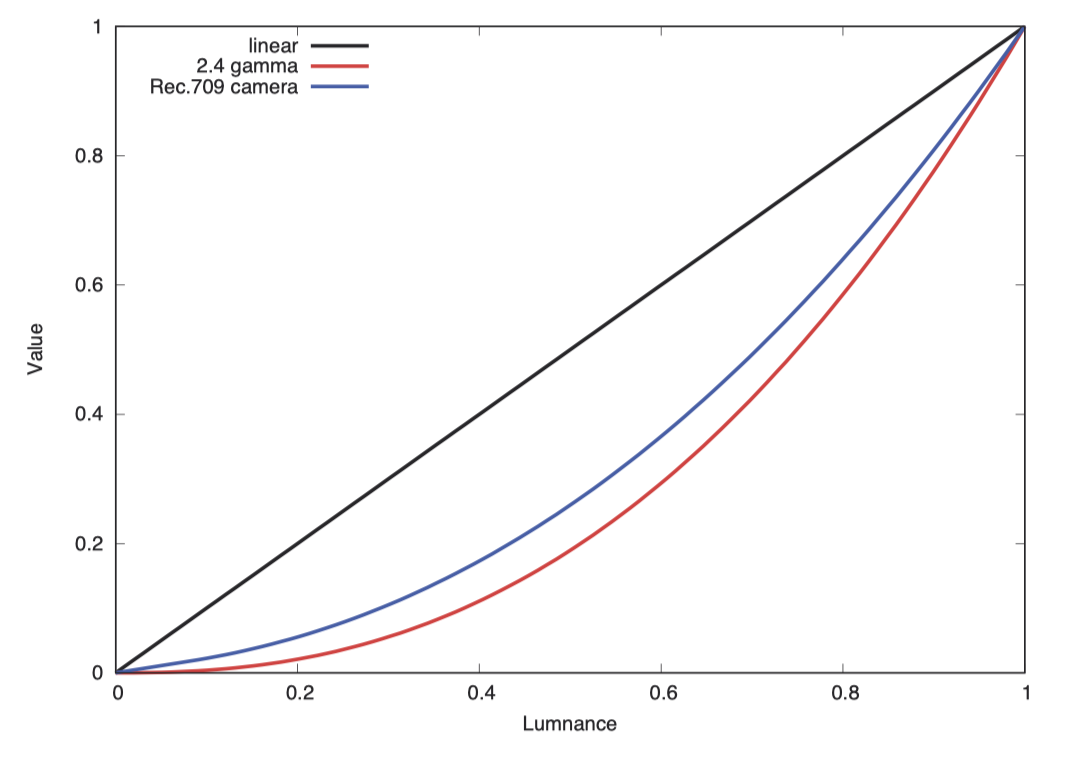
伽马曲线的一个问题是,当亮度接近零时,曲线会趋于完全平坦,这可能会压缩阴影部分的细节。而它的逆函数在接近零点时则变得极为陡峭。此外,函数曲线在零点处截止,而负亮度在实际中并无意义。尽管如此,由于噪声等原因,摄影机的 RGB 值有时可能出现负数。虽然可以裁切掉这些负值,因为负亮度无意义,但这样做会提升阴影区域的平均值。一个理想的色调函数(tone function)应该能以有限的斜率通过原点,并适当延伸以处理负值。例如 sRGB 色彩空间中的色调函数就采取了这种更优的设计。但是,这种改进的方法也有缺点:原点处的斜率选择依赖于具体的显示设备和观看环境,并且低斜率可能导致较大的负 RGB 值扩展。
在下一节中,我们将讨论观看条件,并解读 Rec.709 摄像机曲线。
场景(scene)与显示(display)
Rec. 709 摄像机曲线是针对电视摄像机的一项标准,旨在使电视画面在普通电视机上显示出令人满意的效果。然而,Rec. 709 的色调曲线与电视机设定的 2.4 伽马值并不完全匹配。这里展示了两种色调曲线下的灰阶对比:
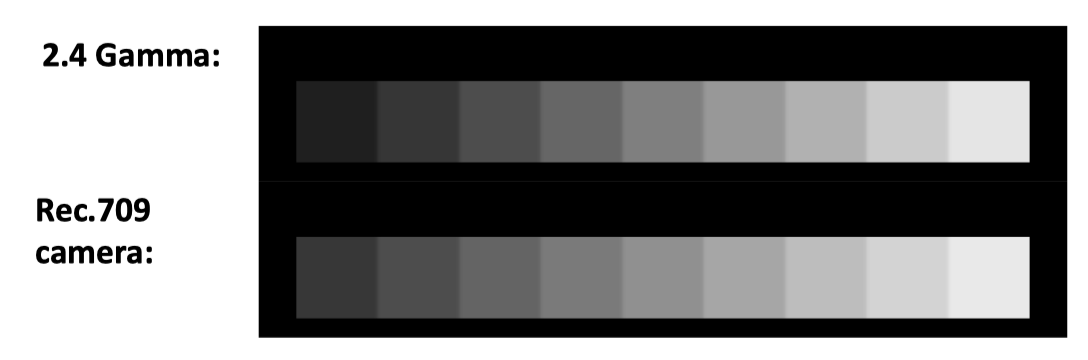
我无法确保你看到的效果与我一致,但我希望这段文字能比图表更直观地说明两者之间的差异。伽马 2.4 色块是按照电视机亮度水平从 0.1 到 0.9 均匀递增的,而 Rec.709 色块则是摄像机拍摄效果在电视上看到的对应亮度水平。尽管高光部分看起来相似,但在伽马 2.4 的电视上,最暗的阴影色调要更暗一些。如果亮度水平进一步降低,对比度的差异将更为明显。
那么,为什么摄像机的输出曲线与显示器的表现不一致呢?这主要是由于观看环境的不同造成的。摄像机拍摄场景时,其周围的光照水平往往与场景本身相当接近。即便是在灯光充足的摄影棚内,也会有一定程度的明亮背景。相比之下,我们观看电视的环境通常是较暗的。标准的电视调色室会在显示器后方设置中性灰墙面,来模拟这种典型的观看条件。在暗背景的包围下,我们可以看到更多的阴影细节,因此,为了使观众的观看体验与摄像师的现场所见保存一致,需要对摄像机捕捉到的阴影部分进行相应的调整。
从历史角度来看,这种设计是有意义的。阴极射线管(CRT)电视固有的 2.4 伽马特性,与我们对灰度的感知正好相匹配。由于电视机的数量远多于电视摄像机,从经济角度而言,在摄像机端应用昂贵的模拟色调校正(analogue tone correction),比应用于电视机端更为合理。此外,在过去,人们不太可能将笨重的 CRT 电视机搬到户外,因此假设暗环境的观看条件是合理的。而在如今,我们可以在户外用手机观看电视节目,且手机的 OLED 或 LCD 屏幕配备了数字色彩校正功能。如果在今天重新发明广播电视系统,我们可能会在显示设备中内置更多关于观看条件(viewing conditions)的校正措施。
电影胶片同样内置了对周围环境的校正机制。电影无论是在外景还是明亮的摄影棚拍摄,最终都要在黑暗的电影院中播放。黑白胶片洗印厂基于过去成功经验的积累,逐渐确定了一种受观众欢迎的色调曲线。彩色胶片不仅需要应用这样的色调曲线以适应黑暗的影院环境,还需要保证三基色通道之间的正确平衡,以实现中性色(neutrals)和肤色(flesh tones)的准确还原。所有这一切都在没有计算机辅助的情况下通过湿法化学(wet chemistry)过程完成,足见彩色胶片的制作堪称非凡成就。
伽马测试图
下图是一张能够测试显示器伽马值的图片。

这张图片通过其像素级别的细节,提供了一种检测显示器伽马值的方法。如果在电脑上查看,可能需要调整缩放设置以确保准确显示。如果每对列中的左侧一列看起来平滑且均匀,说明显示效果可能是正确的。
要获取这本书的在线版本以及更多相关资源,请访问:www.filmlight.ltd.uk/colourbook
在这张图中,右侧的一对列分别包含黑白条纹和一个灰色渐变色块。观察者需要找到灰色渐变色块与黑白条纹颜色平均值相匹配的高度点。为了更准确地确定这一点,可以先找到灰色色块明显比黑白条纹亮或暗的位置,然后取中间点作为估计值。如果是 LCD 显示器,还需要确保从正面直视这个点,因为颜色会随视角变化。一旦找到了这个点,就可以根据左侧的刻度读出对应的伽马值。
接下来向左的一对列是黑白条纹与 50% 灰度条纹,再向左则是黑白条纹与 25% 灰度条纹,以此类推。虽然理论上不同的灰度水平测得的伽马值应该大致相同,但在阴影部分可能会有所波动。此外,在非常低的亮度水平处,由于这张图假设显示器的 0% 黑位水平为纯黑,而实际显示器的“黑色”可能并非绝对纯黑,因此最终的伽马值可能与预期有所偏差。
对于电脑屏幕上的图像,预期的伽马值应该是 2.2 左右。如果是通过印刷版查看,期望值也应该接近 2.2,但不确定因素要更多。如果实际测得的伽马值并不完全符合预期,不必过于担心,可能是文档浏览器或电脑设置的问题,而非显示器本身的问题。这个过程说明,尽管存在一些不确定因素,但依旧有可能只利用一张图像和肉眼来评估显示器的伽马值。
CIE L*a* b* (CIELAB)
CIE L*a* b* 色彩空间是 1976 年基于 CIE 1931 XYZ 色彩空间发展而来的,其中的颜色是使用如下函数
函数
将
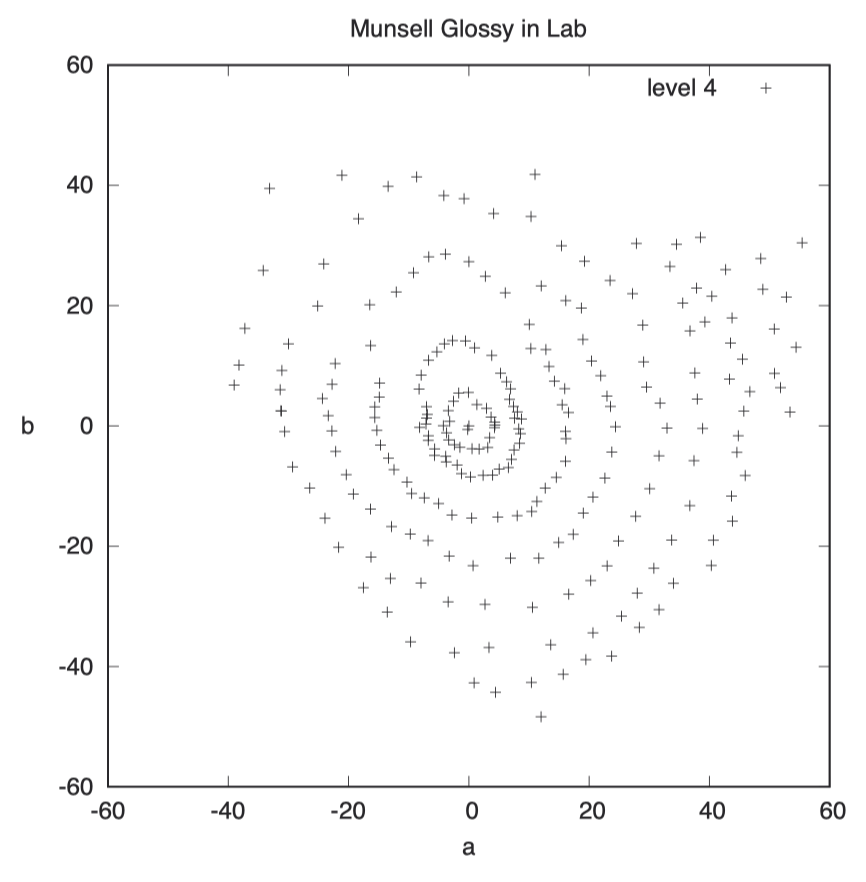
在上图中,孟塞尔色卡的 a, b 坐标分布不是圆形的,但这已经是我们目前构建的最接近(感知均匀)目标的空间了。其中,白色位于坐标原点位置。
L* 值在从 10 降至大约 3 的范围内保持线性。对于反射材料而言,低于 2 的 L 值已经相当暗淡了,即使是最亮的光泽表面也很难达到 1% 以下的反射率。CIE L* a*b* 空间在显示设备领域应用广泛,一台优秀的显示设备应该具备超过 1000: 1 的对比度,这意味着其暗部反射率必须控制在 0.1%以下。在暗部区域观察到一些差异并不奇怪。
L* 值的范围从 0(黑色)延伸至 100(白色),虽然理论上可以处理大于 100 的值,但在实际应用中其上限应为白色。
a* 和 b* 的取值在 -100 至 +100 之间,但真实可见的颜色可能会超出这一范围。值得注意的是,当彩度(chroma)保持不变时,如果 L 值减小,a*和 b* 的数值也会相应减小,这样可以防止在最暗部因噪声而产生极端色彩值。
尽管这个 L*a* b*空间因其过于简化而不被视为一个色貌模型(Colour Appearance Model,CAM),但 CIECAM-02 等更复杂的色彩空间也采用了与其相似的构造原理。
需要注意的是:CIE L*a* b*色彩空间也被称作 CIELAB,这种简称有助于避免文本格式中字符 * 带来的问题。CIE 选择了 L*、a* 和 b* 这三个坐标,是为了避免与 1948 年由亨特(Richard S. Hunter,1909-1991)定义的 Hunter Lab 色彩空间产生混淆。我个人从未使用过 Hunter Lab 色彩空间,你可能也很少会遇到有人使用它。如果有人提及“Lab”,他们很可能是指的 CIELAB 色彩空间。
CIE 2006 标准中的 tRGB
tRGB,或称为三角形 RGB(triangle-RGB),是一种非标准色彩空间,由 CIE 2006 LMS 色彩空间衍生而来。
首先,通过缩放 LMS 值,我们得到了归一化的 lms 值,其中 l+m+s = 1.0。随后,可以将这些 lms 值表示为质心坐标图(barycentric plot)上的点:
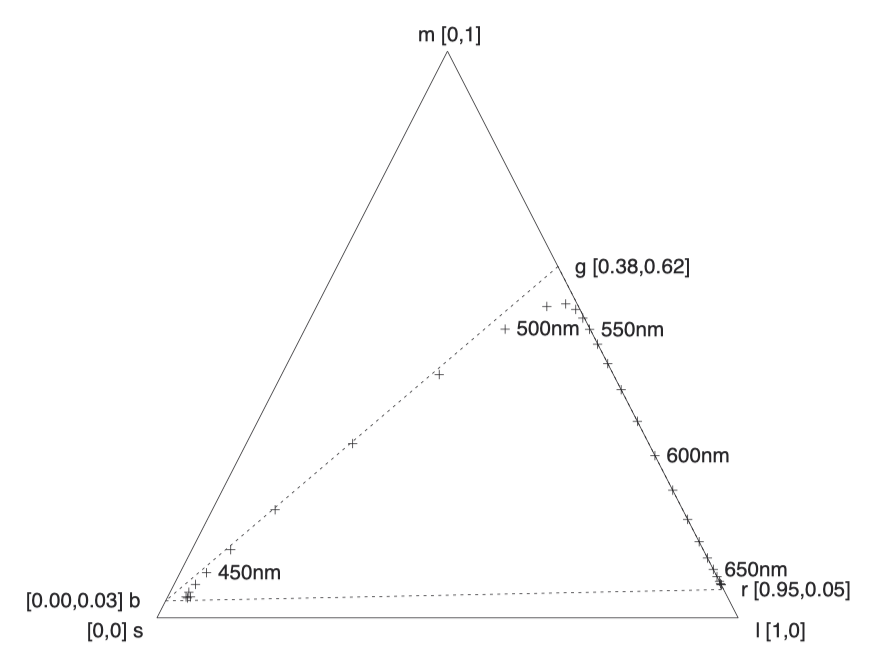
在这个三角形中,“m”是从底边计算的高度,在底边线上为 0.0,顶端为 1.0;“l”和“s”的数值则通过类似的方式从另外两条边上衡量得出。因为这是一个等边三角形,所以 l、m、s 三个数值的总和必须等于 1.0。
我们将从 400 纳米到 700 纳米单波长光对应的 LMS 值在这个三角形内标出各个点,这个形状称为光谱轨迹(spectral locus)。如果将轨迹的起点和终点相连,就形成了一个封闭的形状,该形状内包含了所有真实可见的颜色。形状外的任何点都代表了非真实颜色,无法仅用非负值组成的光谱来生成这样的 LMS 值。
我们在光谱轨迹外围画了一个三角形,其三个顶点分别标记为“r”、“g”和“b”。这三个点并不代表真实存在的颜色,但这个三角形内部大约 94% 的区域是由真实可见的颜色构成的。
我们可以用以下公式在 lms 和 rgb 之间转换:
同样的矩阵也可以用于未归一化的 LMS 与 tRGB 之间的转换。
下图是对之前三角形的一个拉伸版本。我将“r”点移到了右下角,“g”点移到了左上角,而“b”点则移到了左下角。这样的调整导致右上角的三角形区域包含了所有不存在的颜色,而左下角的三角形区域主要包含真实颜色。
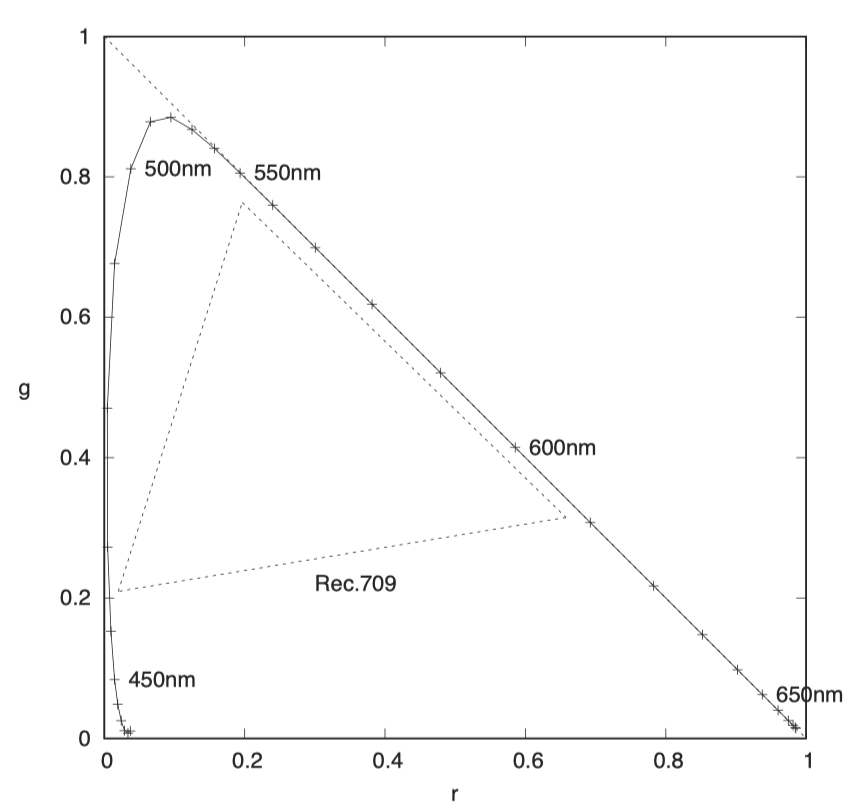
在这个三角形内部,我还绘制了 Rec.709 视频色域。还有一种称为 Pointer 色域的不规则形状,它包含了大量真实场景中的所有颜色,我将在第七章对其进行详细绘制。Rec.709 色域的设计使其能够完全包含在 Pointer 色域内部。此处选择绘制 Rec.709 色域而非 Pointer 色域,是因为其形状简单,可以使图表更为清晰易读。
图中的横轴和纵轴代表了新的彩度坐标 r, g。在三角形的底部,我们可以看到一个包含紫色(violet)、紫红色(purple)和深红色(deep red)的广阔区域。光谱轨迹的闭合边缘是由 400 纳米和 700 纳米波长的单色光混合而成的。人眼对这两种波长并不敏感,如果这些颜色出现在反射物体上,将显得非常暗淡。在现实场景中,你几乎不可能找到 g 值低于 0.1 的像素。
最后,我们可以利用以下公式从 LMS 直接计算出 r, g 的值:
以上两个值定义了彩度(chroma)。第三章还有一个从 LMS 生成光亮度 Y 值的简单公式:
将这些公式结合在一起,我们就得到了一个类似 CIE Yu’v’ 色彩空间的 Yrg 色彩空间。
这个概念并不是全新的。下图是物理学家卢基什(Matthew Luckiesh,1883-1967)1921 年著作中的的麦克斯韦三角形(Maxwell’s triangle)。他采用了质心坐标图,通过调整 B 和 G 顶点的位置来确白色位于中心。将这个三角形翻转并适当拉伸,就形成了我们现在的图表。
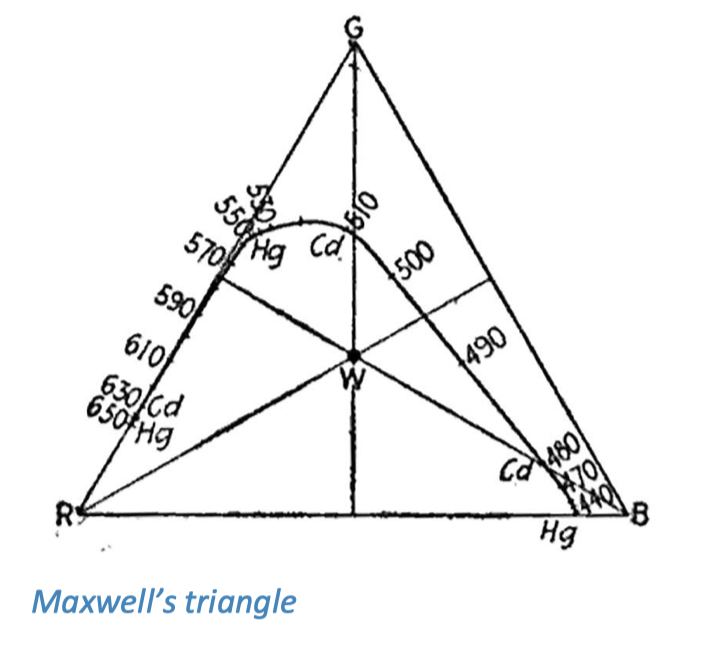
我们在新的 r, g 轴上绘制了孟塞尔光面色卡(Munsell Glossy)第 4 级的颜色,并针对 6500K 白点进行标定:
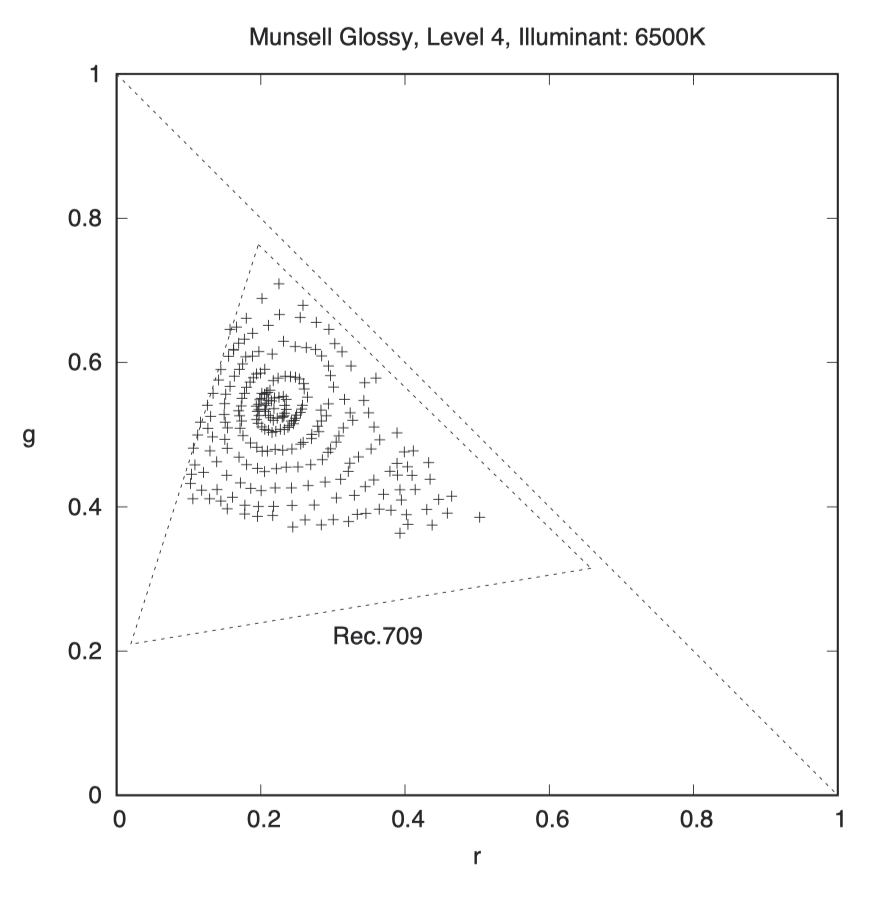
我并不明白为何彩度(chroma)会呈现出类似感知均匀空间的圆形分布,但实际情况确实如此。将红色与蓝色放在对角线上,并将绿色放在原点时,就不会出现这样的情况。r, g 轴的设计还意味着,长对角线上的一端是红色,另一端是绿色,中间是黄色,而不是简单地将它们压扁在同一个轴上。
在这个色彩空间中,我们选择的白点并无特殊之处。不妨换一个白点试试看:
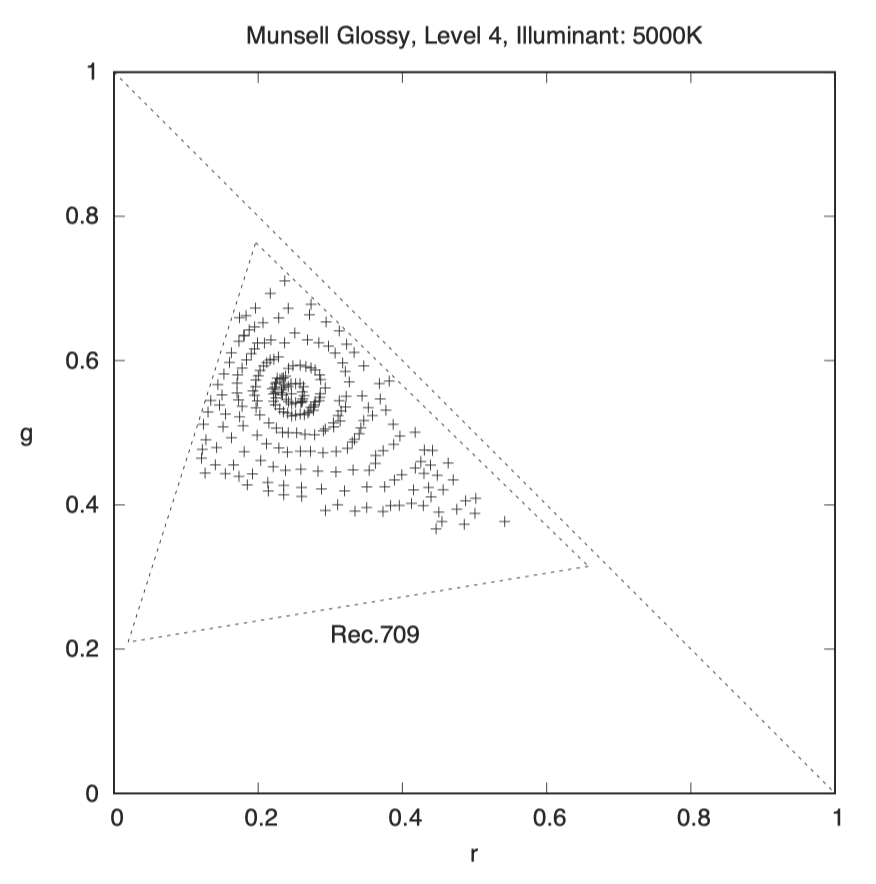
与 D65 相比,这些圆形看起来更加饱满。虽然我没有直接证据表明孟塞尔色彩空间曾经特意匹配过 D50 白点,但鉴于 D50 长期以来一直是反射观察灯箱(reflection viewing booths)的标准光源,它可能对孟塞尔空间产生了一定影响。
再换用钨丝灯光做一次实验,看看会有什么不同:
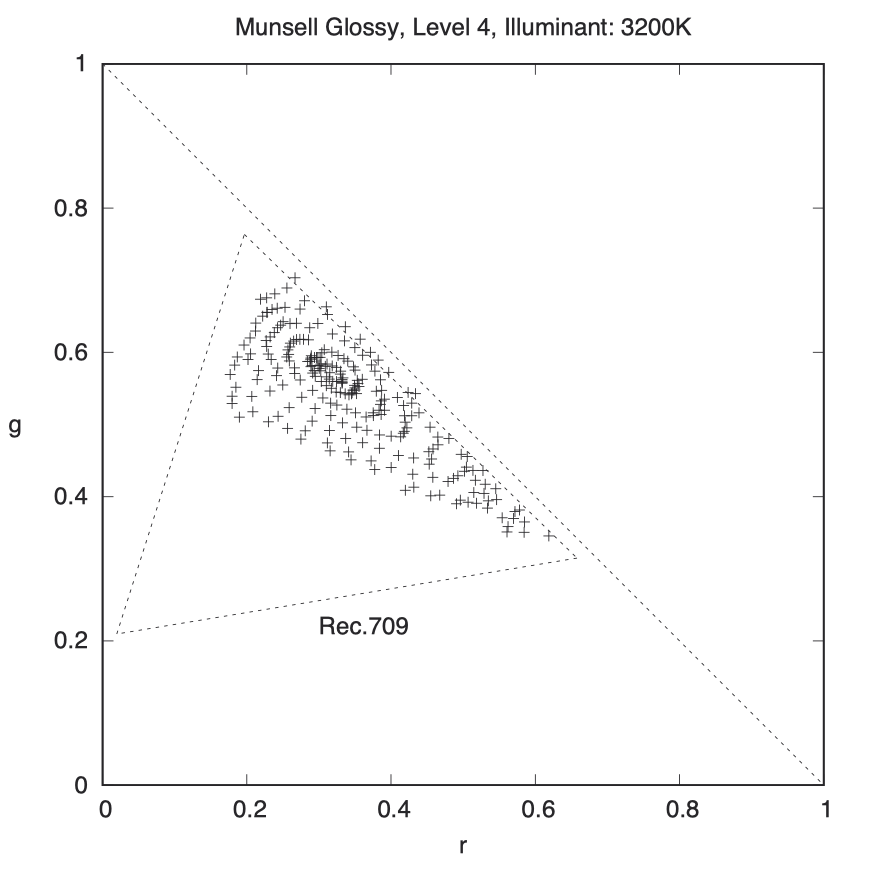
对于钨丝灯照明,我们并不期待看到圆形分布。孟塞尔色彩空间对于 D65 至 D50 之间的白光是均匀的,但对钨丝灯光则不太适用。果不其然,我们没有看到圆形图案,这说明一切正按预期工作。
我们也不期望看到过多的蓝色对比度。蓝色顶点位于原点,可以观察到这些颜色点有远离它的趋势。有些黄色点甚至超出了 Rec.709 色彩空间的范围。
接下来的图标展示了 tRGB 的权值分布。在这里,基于 LMS 权值,我们构建了 tRGB 或称之为“三角形 RGB”的基色,并通过一个矩阵转换来得到 r, g 彩度。
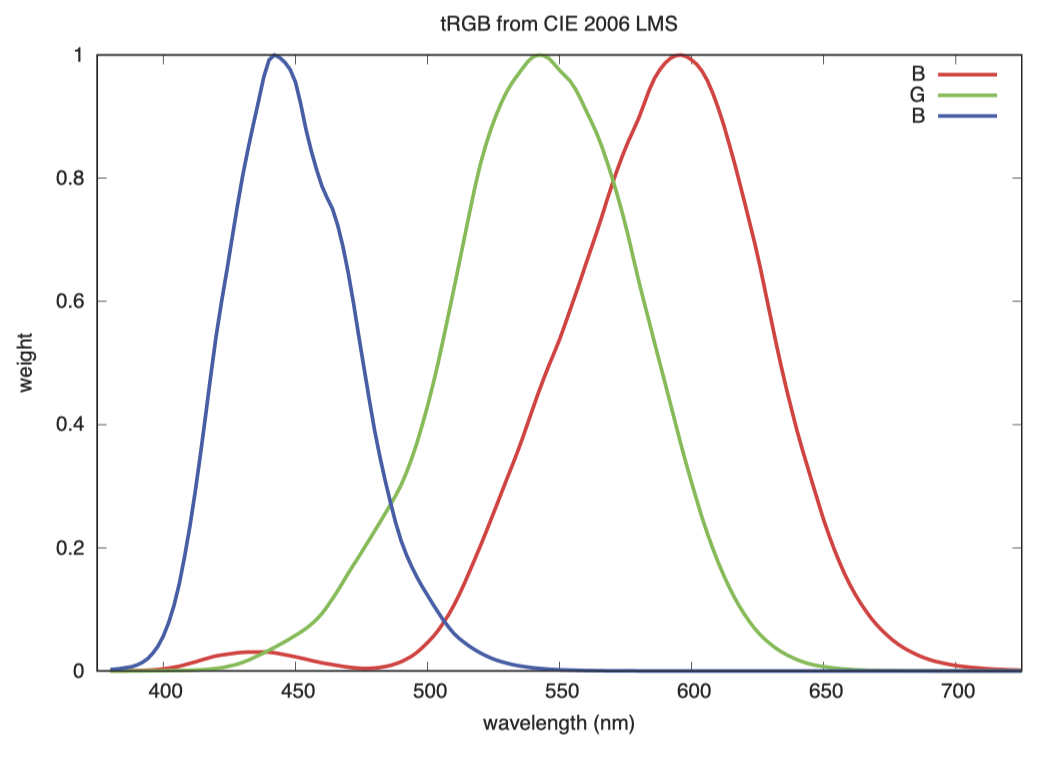
在 LMS 色彩空间中,M 曲线和 S 曲线之间的分离度较小。XYZ 的 X 曲线在蓝色区域有一个明显的第二峰值,而在当前图标中,我们看到 R 和 G 之间有良好的分离,而且 R 曲线只有一个很小的第二峰值。这些曲线与摄影机的基色响应曲线很相似,这再次说明一切都在按照应有的方式运作:多年来人们在制造摄影机时,不仅调整了 RGB 滤色片以实现良好的色彩分离,也力求让摄影机“看到”的颜色与人眼所见相一致。
从 tRGB 衍生的 tLAB
与 CIELAB 不同,LMS 并没有官方的亮度-彩度(luma-chroma)空间,这实在是有些遗憾,因为 LMS 代表了一种更先进、更现代的三刺激值系统。接下来,我们尝试构建一个自己的版本:
CIELAB 通过光亮度 Y 值来计算 L 值。在第三章中我们介绍了一个简易公式,可以从 LMS 计算出光亮度 Y。所以,我们可以用这个公式来计算 Y 值,再采用 CIELAB 的方式来计算 L 值。
之前 r, g 彩度轴上的孟塞尔色彩点形成了漂亮的圆形分布,于是我们借鉴其计算方法:
与 CIECAM 的 a, b 不同,r, g 白点并不位于原点。因此,我们需要减去白点的数值,以便把它放到正确的位置上。
Δ r 和 Δ g 轴相对于常规的 a, b 轴偏转了 45 度,因此我们需要旋转它们,让红色沿着主轴排列。同时,为了模拟 CIELAB 在低亮度颜色中降低彩度的方式,我们按 L 值进行缩放。在首次尝试中,我将这两个轴都扩大了 4 倍,以适应 CIELAB 的 a, b 取值范围:
这种方法对于 D65 和 D50 下的孟塞尔色彩点能够形成良好的圆形分布,但在 3200K 钨丝光源下,我们在 b’ 轴的对比度远低于 CIELAB b 轴的对比度。在第二次尝试中,我为 a 轴设置了固定的缩放比例,并根据白点调整了 b 轴的缩放比例:
其中:
D65 光源下的
我们来验证一下这种方法的有效性。在 tLAB 和 CIELAB 色彩空间中绘制孟塞尔色彩点。
以下是在 3200K 白光条件下,在 tLab(实心圆)与 CIELAB(空心圆)色彩空间绘制的孟塞尔色彩点:

tLab 色彩空间的中心形状并不是完美的圆形,CIELAB 色彩空间同样如此。实际上,它们都呈现出类似的“D”形状(在合并的图标中可能不太明显)。除了红色区域似乎扩展得过远之外,tLab 中的饱和色彩分布显得更为均匀。
以下是一个采用 D65 白点的类似图像。

tLab 空间与 CIELAB 空间的相似之处在于,其白点位于(100, 0, 0),红-绿轴水平分布,蓝黄轴垂直分布。在 L 值和 a, b 值上的等距变化能产生均匀的视觉对比度。但是,在点的分布上我们观察到一些差异:青色区域的边缘相比于理想情况稍微紧凑了一些。如果要将其拉伸至理想状态,则需要进行非线性变换,而这将破坏 tLab 空间 a, b 彩度(chroma)的线性特性。这意味着在
tLab 色彩空间尚未被任何标准机构正式认可。如果你采用 LMS 而非 XYZ 色彩空间工作,则 tLab 与 CIELAB 具有相似性,并且计算公式较为简洁。
恰可察觉差(Just Noticeable Differendce, JND)
我们迄今为止创建的色彩空间,都是通过将从白到黑或从灰到红的色域均匀划分为具有相同色彩对比度的明显色阶来实现的。
还有一种不同的方法。可以通过对比一种颜色与其周围颜色,确定它们之间的恰可察觉差(Just Noticeable Differences,JND),这通常需要在暗室中仔细观察 2 度标准观测者视场来进行试验。当绘制出与中心颜色难以区分的颜色轨迹时,它们通常表现为椭圆形,这种椭圆称为麦克亚当椭圆(MacAdam Ellipsis),是以麦克亚当(David Lewis MacAdam,1910-1998)在 1942 年发表的论文而命名的。
由于麦克亚当椭圆过于微小,为了清晰观察,一般需要以一定的比例放大绘制。下图展示了在我们的 r, g 色彩空间中,以 5 倍的放大倍率绘制的 1942 年原始版麦克亚当椭圆。
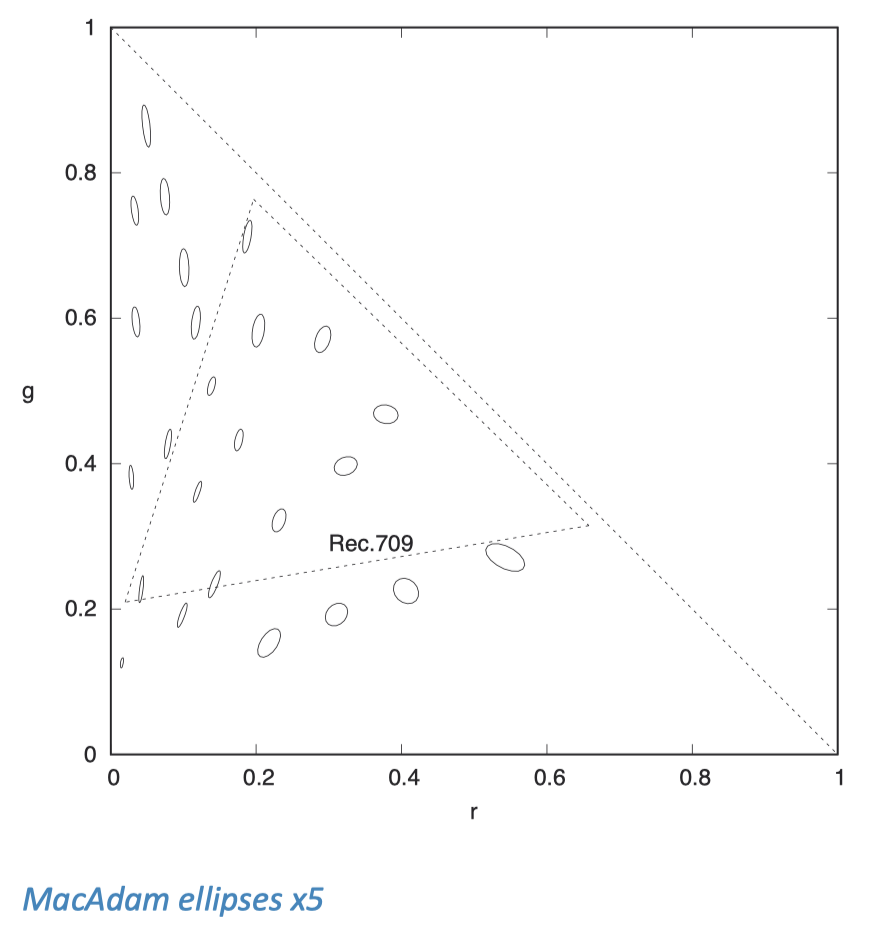
我不清楚麦克亚当使用的具体光谱数据,因此在将其转换到 r, g 坐标系时可能存在一些微小误差。任何误差可能都是长期性的:它们可能会稍微移动椭圆的位置,但对椭圆形状的应该影响不大。
这些椭圆在色彩空间中覆盖了比我的孟塞尔数据(Munsell Data)更多的区域,特别是在左边界和下边界附近,我没有任何数据点靠近这个区域。即便在我有限的数据中,也没有观察到在麦克亚当的图表中出现的那些扭曲现象。我推测这可能是一种只能在暗室中精确测量,但在实际图像中难以察觉的现象。我之所以提及恰可察觉差,是因为相关的研究论文颇多,你在搜索时可能会遇到,但我认为它们对于我们想要在图像处理方面达成的目标帮助不大。
Delta E(△E)
这里不打算深入讲解微积分,但为了帮助数学背景较浅的读者理解,我们简单介绍一下希腊字母 delta(
在颜色领域,
在 CIELAB 色彩空间中,两组颜色值
一个恰可察觉差(JND)对应的
我们也为 tLab 色彩空间定义了一个相似的公式:
下面的色觉测试图包含了六个随机排列方向的“T”字形,当在 Rec.709 视频 RGB 色彩空间下展示时,其色差对应的
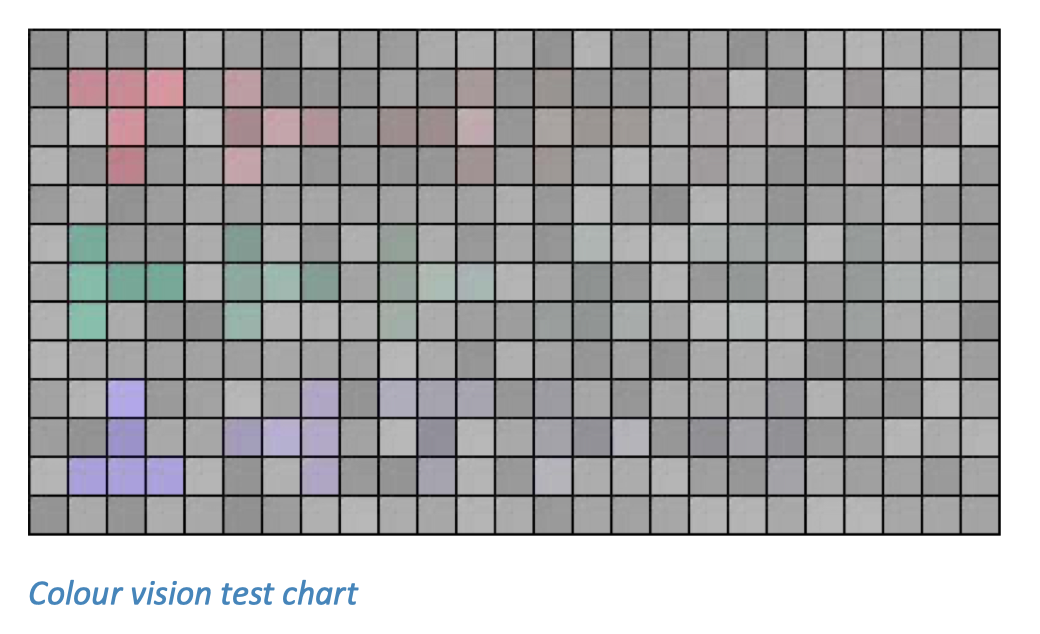
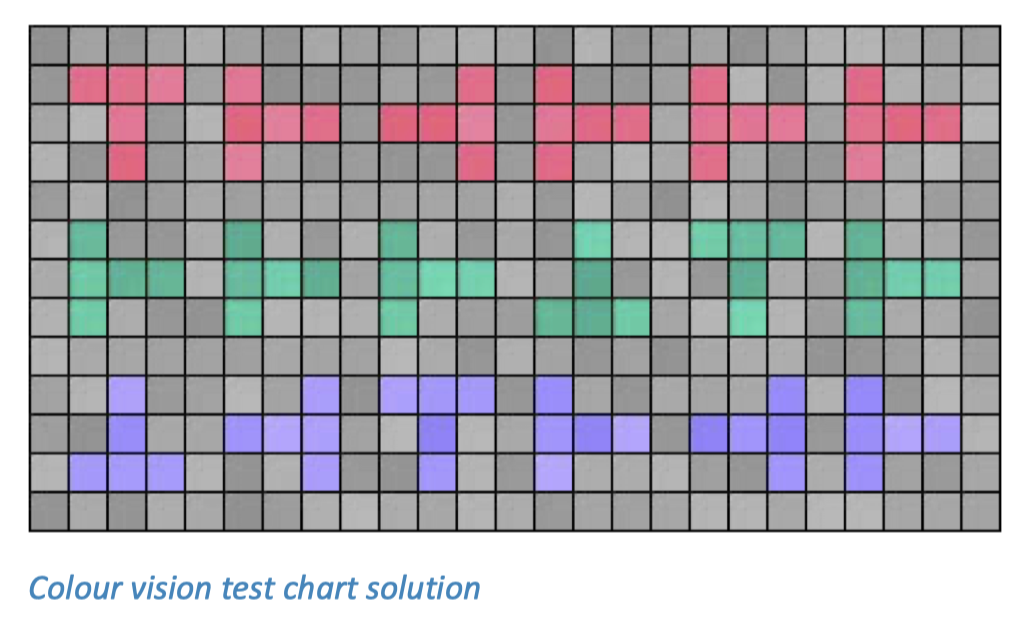
在该图表中,三行图案旨在展示 L、M 和 S 视觉通道的对比度差异。你可能需要放大查看,特别是在底部一行,因为需要依赖周围视觉来检测 S 视锥细胞的敏感性。答案会在下一页给出。
我无法清晰地看到最后一列。如果我不知道这里有形状,我可能根本不会注意到它们。但如果知道其中一个方向存在,大部分情况下我都能识别出正确的方向。
1976 年提出的
我没有详细介绍最新的
主波长(dominant wavelength)
主波长这个概念虽然经常出现在书中,但我个人并未发现其特别有用。假设你有一种颜色(浅绿色)和一个白点(D65)。在 x, y 坐标系中,浅绿色可能恰好位于 D65 白点与光谱轨迹上的 520 纳米纯绿色的中间位置。这意味着,我们可以通过混合 D65 白光和 520 纳米的绿光来得到浅绿色。这里的 520 纳米就称为浅绿色的 主波长(dominant wawelength)。相反,如果我们选择了粉色,那么就没有能够与 D65 白光混合的主导波长。但是,如果我们将这条线穿过白点延伸,它会在光谱轨迹上与 互补波长(complementary wavelength) 相交。这个互补波长就是我们需要与粉色混合以产生 D65 白光的波长。对于粉色而言,其互补波长可能是 520 纳米的绿色。主波长和互补波长都取决于我们选择的白点。
这种色彩空间并非均匀,从红色到紫色这一段的色彩要么是基于互补波长的,要么是基于我们几乎无法察觉、也可能测量得不够精确的极限波长的混合。
均匀色彩空间
在本章中,我们讨论了如何基于三刺激值(tristimulus)来量化我们对亮度、色相、饱和度的感知。虽然三刺激值建立在扎实的科学基础上,但对于这些感觉的量化很大程度上仍依赖于猜测,因为这些感觉存在于我们的大脑中,而非可以直接测量的实体。由于我们所见的颜色不仅取决于颜色本身,还受到周围环境的影响,因此试图创建一个完全准确且与人类感知相匹配的均匀色彩空间,从一开始就是注定困难重重的。不过,一些研究的成果已经足够良好,可以在实践中应用了。
对颜色对比度的估计有两种截然不同的方法。第一种方法是通过观察明显可见的对比度,并通过主观判断进行匹配。这种方法对于视亮度(brightness)而言较为简单,对于色相(hue)和色度(chroma)也并非难事。这种方法基于实际对比的结果,对艺术家而言会感到很熟悉。第二种方法则是确定恰可察觉差(JNDs),这就是麦克亚当椭圆的确定方式。这种方法客观性强,但执行起来较为困难,不是简单地在观察灯箱(viewing booth)中对色卡进行排序,而是在黑暗实验室的严格受控条件下估计微小的对比度差别。这些结果对艺术家来说可能显得陌生,这或许是因为这种检测阈值是由视觉信号链早期的信噪比限制所决定的。这种方法对于研究视网膜神经节细胞很有帮助,但在艺术评价方面则不太适用。
当前可用的均匀色彩空间包括:
孟塞尔(Musell)色彩空间:基于真实色彩,无公式(尽管有模拟实现),依赖光源类型,作为评估其他色彩空间的基准很有用。
Yxy 色彩空间:虽然色度和亮度不均匀,但有独立的视亮度(brightness)和彩度(chroma)两个维度。
Yu’v’色彩空间:亮度 Y 轴不均匀,色度 u’v’ 轴接近均匀,计算公式相对简单。
CIELAB 色彩空间:基于早期 XYZ 色彩空间,在大多数白光条件下具有良好的均匀性,广泛用于多种应用场景。
Yrg 色彩空间:基于新的 LMS 色彩空间,未成为标准,亮度 Y 轴不均匀,r, g 轴在 D50 到 D65 范围内的白光下相对均匀。
tLab 色彩空间:同样基于新的 LMS 色彩空间,未成为标准,但在多数白光条件下具有良好的均匀性。
- 1.在色度图(如CIE 1931色度图或CIE 1976 UCS色度图)上,随着黑体温度的变化,其发出的光颜色也会变化,形成一条连续的曲线,这条曲线被称为“黑体轨迹”或“热轨迹(Thermal Locus)”。从低温到高温,黑体颜色会从红色逐渐过渡到橙色、黄色、白色,再变为蓝色。 ↩
转载请注明来源。欢迎留言评论,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。