由 Filmlight 公司的色彩科学专家理查德·柯克(Richard Kirk)撰写的色彩科学白皮书《颜色:感知与测量》(Colour: Sense & Measurement)第三章(翻译初稿)
译者:Horace Lu
原书下载地址
在上一章中,我们探讨了光的测量方法。我们通过波长(以纳米为单位)来区分单色光。通常,人眼能够看到的光波长范围在 400 到 700 纳米之间。我们通过将每个波长的光能转化为热能,并将其换算成瓦特(Watt)值,来量化不同波长处的光强。光谱(spectrum)则展示了各个波长的功率。虽然我们命名了一些不同的波长,以便确定正在讨论的颜色,但对人类视觉的深入讨论并未展开。本章,我们将深入探讨如何将上章提到的测量工具和技术所得到的数值,与我们实际看到的颜色联系起来。
光的混合
在上一章,我们为特定波长的光指定了颜色名称。黑色代表“无光”(zero light)。至于白色、灰色、粉红色(pink)、棕色(brown)或浅蓝色(light blue),我们还未进行讨论。
亚里士多德尝试通过混合不同颜色的沙粒、交织不同颜色的纱线,或在白色大理石上用木炭画出黑线或黑点等方法,来探索颜色的混合:

他熟悉马赛克艺术家使用的半调(half-toning)技艺,这种技艺可以从有限的矿物调色板中创造出平滑细腻的色阶(shade)。他观察到,虽然织工们可以在灯光下编织图案,但他们总会在日光下核对图案的外观,因为某些颜色的组合(如紫色和素色),在不同光线下会呈现出不同的视觉效果。他并不认为混合黑色和白色得到的灰色是一种绝对的颜色,而是认为这种灰色是特定混合过程和照明条件的结果。但是,如果从这个灰度范围中选择两种色调,就可以重复这个混合过程:

就像在平面几何中可以将一条线无限地分割成更细小的线段一样,我们也可以将任意两种颜色之间的差异细分为无数个色调(tones)。这种细分方式是亚里士多德时代人们对无限概念的一种直观表达。虽然我们可能无法区分这种无穷细分后的颜色变化,但构建这些色调是可能的。
亚里士多德使用木炭在大理石上绘图的方法实际上颇具巧思。如果将一半的表面涂上细木炭粉末,你也许会预期它能够反射一半的光线。但像纸张和大理石这样的白色物质是半透明的。光线在其内部反弹,入射和出射的路径并非总是相同。这意味着木炭可能在光线进入时吸收了一半的光线,在光线出射时又吸收了剩余光线的一半,因此它实际上只反射了四分之一而非一半的光线。我们将在第 10 章再来讨论这个话题。亚里士多德或许未能了解这些具体细节,但他足够聪明地用一般术语定义了他的调色过程,因此无论怎样,他的理论都站得住脚。
亚里士多德还探讨了需要几种基本颜色才能混合出所有其他颜色。他依次列出了七种颜色:

不同于牛顿的七种颜色,亚里士多德定义了另外七种颜色的组合,把黑色和白色也包括了进来,并且将所有颜色按特定顺序排列在一起。是否所有颜色都可以视为白色和黑色的混合体?有人是这样解读亚里士多德的。但我很难相信这个解读,因为亚里士多德显然已经探索过白色和黑色混合是怎样的。我们可以在 SMPTE 彩条(SMPTE Colour Bars)中看到类似的颜色排列:

我更愿意认为,亚里士多德是根据他所感受到的视亮度(brightness)对颜色进行了排序。他对中间部分颜色的排列顺序与 SMPTE 彩条有所不同,这可能是因为他对当时可用颜料的了解有限——没有一种颜料能像视频标准中的绿色那样鲜艳。他对颜色的描述只通过名称来体现。对我们而言,尝试猜测 1730 年牛顿所说的“蓝色”对应哪种颜色是很难的,而尝试推断亚里士多德在公元前 350 年命名的颜色含义,则更是难上加难。
古希腊语 κυανοῦν(kúanon)可能曾经意为“明亮”或“闪耀”,或许指的是是像天空那样的明亮,而并不是天蓝色(sky blue)。荷马使用 κύανος 形容赫克托耳的头发(在其他地方他称之为“黄色”),但荷马的希腊语比亚里士多德时代的希腊语要古老得多。κύανος 的另一层意思是指较深的矿物质的蓝色,可能来自赫梯语的“kuwannan”(意为“宝石,铜,蓝色”)。这个用法是在荷马之后很久才出现的,可能与亚里士多德的理解相符。如果你想尝试从颜料中混合出所有的颜色,那么你需要一种深蓝色(dark blue),但可以尝试混合青色(cyan)来实现。
亚里士多德是否对亮度(brightness)有着超前的理解?这一点我无从得知。虽然在此处这并不重要,但想象他可能在托马斯·杨之前两千年就接近于发现第八种颜色,并将这些颜色置于一个立方体的角落,还是一件颇具启发性的事情。
三色近似理论(the three-color approximation)
让我们回到光的混合问题上。我们可以测量光的波长,并且可以使用标准单位来量化特定波长的光的强度。接下来,我们可以通过调节两种特定波长的光的强度来制造两种波长的混合光。以 650 纳米的红色和 530 纳米的绿色为例,它们的半调混色(halftone mixture)效果可能如下所示:

在混色的两端,我们观察到了鲜亮的红色和绿色,中间部分则呈现出一种棕色调。你在中间看到的具体颜色可能取决于阅读这篇文章所用的设备。它看起来不太可能是亮黄色,但如果调高设备亮度,则可能会变成黄色。
现在,让我们把 460 纳米的蓝色作为第三种颜色添加到混色当中。虽然可以尝试绘制一个连续的三色混合的马赛克图案,但为了避免解读上的困难,我们选择以固定间隔为三种颜色的混色结果绘制一系列小圆圈:
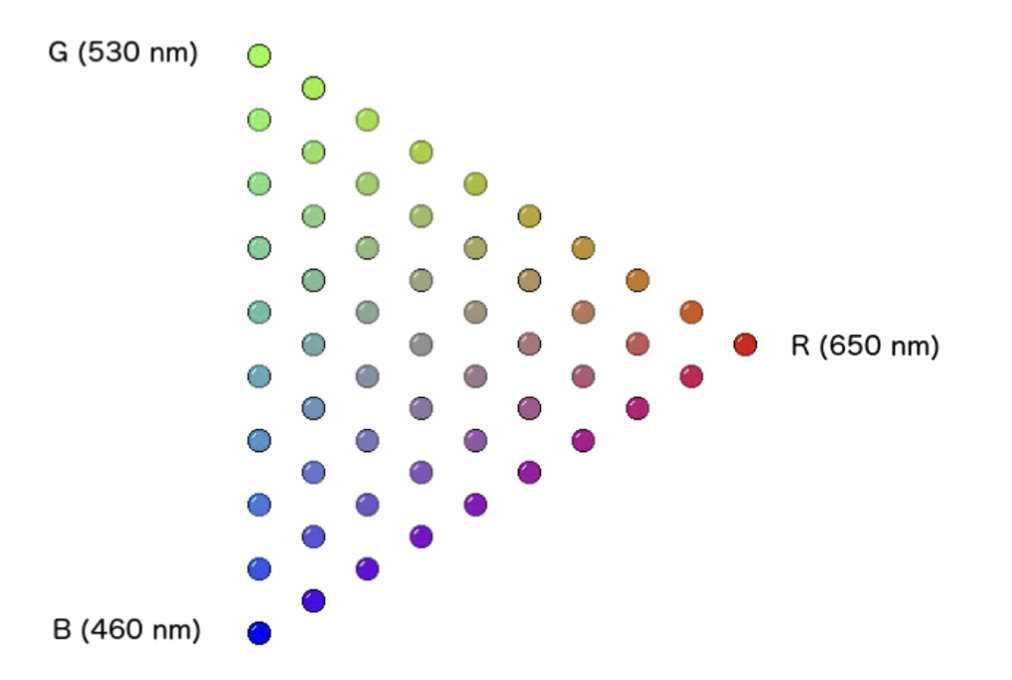
引入第三种颜色后,我们几乎可以得到所有颜色。有些颜色可能看起来稍显暗淡(drab)。在混色中没有纯白色,但中间的那一点呈现出灰色,如果提高亮度则会变成白色。我们或许无法混出像 500 纳米纯天蓝色那样强烈的颜色,但与只有红色和绿色的混色相比,没有哪种颜色是完全缺失的。
托马斯·杨是第一个用科学来解释这种现象的人。他在 1802 年提出,我们的视觉系统可能依赖于眼睛里的三种不同类型的颜色感受器(colour sensor)。如果我们的感受器对红色、绿色、紫色敏感,那么当某个波长同时刺激其中两种受体(receptors)时,我们就能感知到介于两者之间的蓝绿色和黄色。
我将这种解释称为“三色近似理论”。之所以是近似,是因为我们的眼睛并非像摄影机那样装配了统一的 RGB 图像传感器阵列。人眼的构造并非一成不变,我们拥有的感受器类型远不止三种。你甚至可以不借助任何辅助工具,用肉眼观察到光的偏振现象(即“海丁格尔刷效应” Haidinger’s brushes)[1]。在视觉科学领域,三色近似理论依然是一个极为有用的工具。可靠的参考资料十分稀缺,而对于常见的色觉问题,这种理论近似所带来的误差是可以接受的。
三色近似理论的偏差
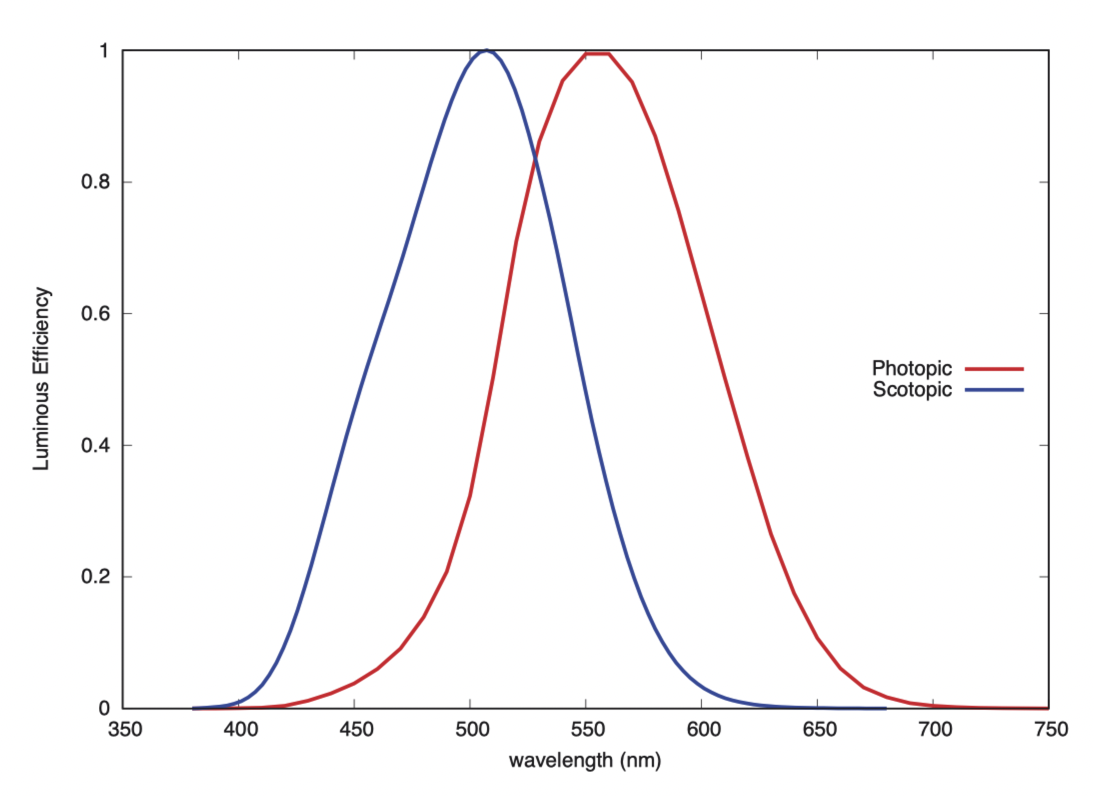
视锥细胞让我们在白天拥有三色“明视觉”(photopic vision)。而我们还有一组视杆细胞,用于夜间的单色“暗视觉”(scotopic vision),这些细胞对于 500 纳米附近的蓝绿色光敏感度最高,不同于视锥细胞敏感度峰值所在的 555 纳米黄绿色。
视杆细胞内含有一种粉红色的色素(感光物质),称为视紫红质(rhodopsin)。1876 年,弗朗茨·克里斯蒂安·博尔(Franz Christian Boll,1849-1879)观察到一只解剖后的青蛙眼中的红色视网膜在光照下是如何褪色(bleach)的。他猜测这种色素的褪色过程是视杆细胞测量光强度的方法。视锥细胞中也有类似的色素,即视紫蓝质(iodopsin),但它们在视网膜死亡时才褪色,因此在开发出能对活体眼内细胞成像的计算机稳定显微镜(computer stabilised microscope)之前,我们无法观察到这些色素。
视杆细胞即使在较强光照下也能提供有效信号。在《色盲岛》(The Island of the Colorblind)中,奥利弗·萨克斯(Oliver Sacks,1933-2015)描述了密克罗尼西亚(Micronesian)平格拉普岛(Pinglap)的故事,那里的许多居民由于近亲繁殖而患有严重的色盲症,完全无法用视锥细胞进行视觉感知。因为他们的视觉中心没有工作细胞,他们的视力非常差,在充足的日光下尤其感到不适,但他们仍然可以只靠视杆细胞在白天看到东西。
没有证据表明,人类将视杆细胞用作第四种颜色受体。在低光条件下,存在一种名为“中间视觉”(mezopic vision)的状态,在这一状态下,我们主要依靠视杆细胞进行视觉感知,同时从视锥细胞中获取有限的颜色信息。视杆细胞对短波长光线的敏感度高于视锥细胞,因此在低明度下,红色显得更暗,而蓝色则显得更亮。这种随视亮度(brightness)变化而产生的颜色变化,称为浦肯野位移(Purkinje shift)[2]。
如果将下面这张图打印出来,红色的斑点看起来应该比蓝色的更明亮。

如果在满月的照射下观看这张印刷品,你应该依然能感知到颜色,但蓝色斑点应该看起来更明亮。这并不是因为月光中的蓝色成分更多(实际上也并没有),而是因为在这种条件下,我们的光亮度(luminance)信号来自视杆细胞而不是视锥细胞。中间视觉是很难模拟的。在电影制作中,我们通过减弱暖色调、调暗中间色调,来模拟低光环境下的视觉效果,从而营造出相应的视觉感受。
在低光环境下,我们面临的另一个挑战是视锥细胞的工作模式。我们的视锥细胞处于“持续激发模式”(tonic mode),这意味着它们不只在接收到信号时才放电(fire),而且在黑暗中也会以较低的频率放电。这就导致很难从暗信号中分辨出一个微小信号,特别是当它与视网膜神经节(retinal ganglia)上相邻细胞产生的其他更大信号相结合之后。
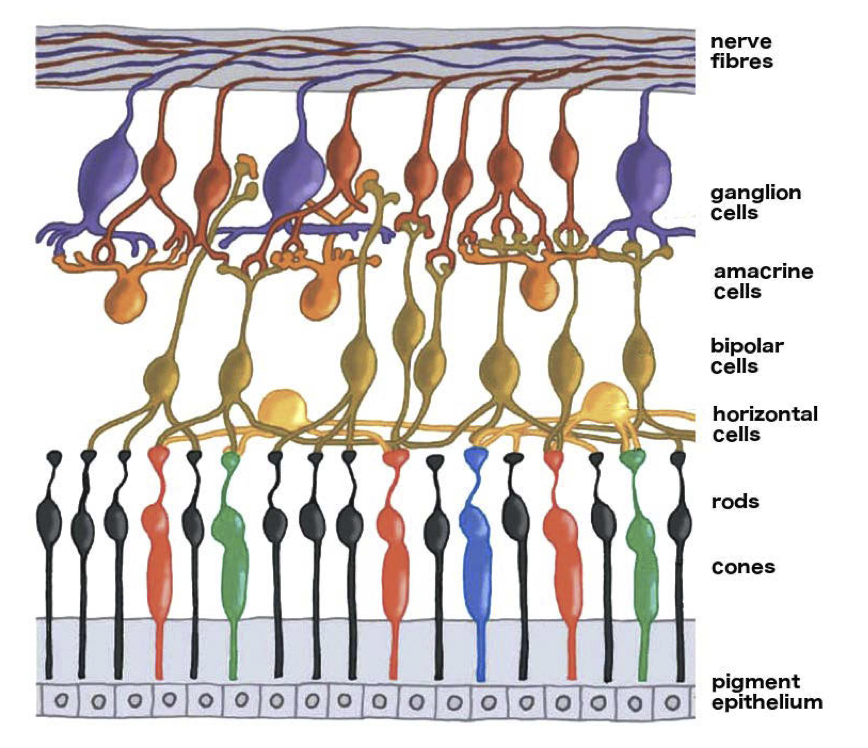
我们将在第 8 章中更详细地讨论视网膜上的这些信号连接。当前我们需要了解的是,视网膜的结构是很复杂的,有很多层细胞将视锥细胞及其相邻细胞的信号结合起来,生成光亮度(luminance)、颜色、边缘、运动的视觉信号。因此,视网膜远不止是一个简单的摄影机 RGB 滤光片阵列那么简单。
视网膜并没有保留到达 RGB 探测器上的绝对光量,这一事实可能初听起来有些奇怪。在上图所示的视网膜结构中,光线首先从顶部进入,随后要穿过一系列神经细胞,才能到达位于底部的探测细胞。虽然这些细胞是相当透明的,但它们对光线有一定的散射作用。此外,视网膜表面还有血管网络。色素上皮细胞(pigment epithelium)能够吸收一些散射光,但由于眼睛内部并非全黑一片,总会有散射光存在,因此在视锥细胞上很难有一个准确的暗电平(dark level)。
至此,我已经介绍了对红色、绿色、蓝色敏感的视锥细胞,现在是时候开始采用标准化的命名了。这三种视锥细胞被称为 L、M、S,其中 L 代表长波长(Long)的红色,M 代表中波长(Medium)的绿色,S 代表短波长(Short)的蓝色和紫色。
贝佐德-布吕克效应(The Bezold-Brüke effect)
在如月光这样昏暗的光照条件下,我们能够辨识出红色(L)和绿色(M)。当 L 和 M 信号大致相等时,我们能看到黄色(L+M)。当其中一个信号比另一个信号大得多时,我们会很难区分橙色和黄绿色的细微差别(shade)。这是贝佐德·布吕克效应的体现,即:我们看到的颜色会随光照强度的变化而改变。
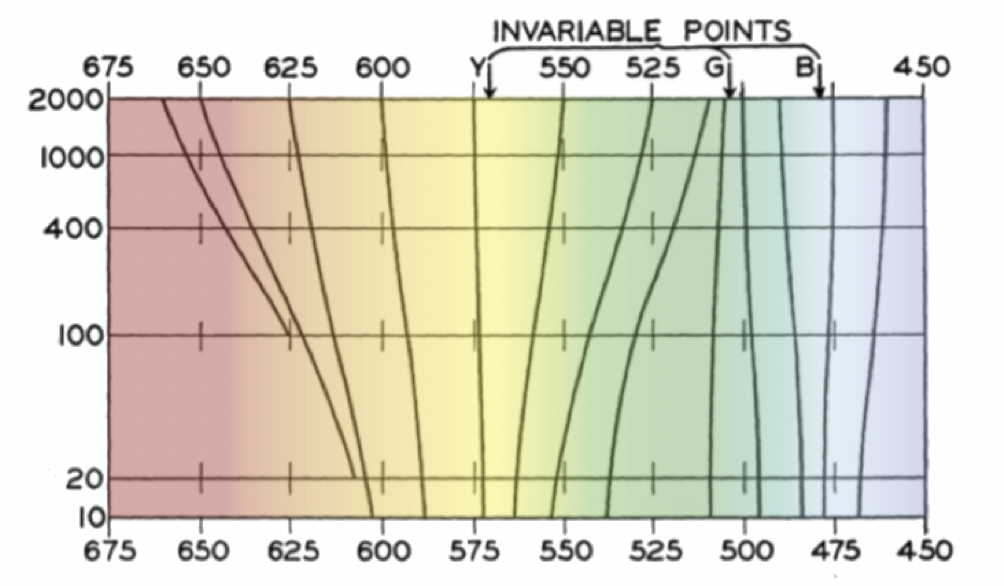
贝佐德(Wilhelm von Bezold,1837-1907)和布吕克(M. E. Brücke)在 19 世纪末测量了这种效应。上图绘制于约 1940 年,横轴表示波长(纳米),纵轴表示视亮度(brightness),单位为特罗兰(Troland,tr [3])。图中的颜色是后来添加的,显示了在良好照明条件下我们可能看到的颜色。轮廓线连接了从视觉上看起来颜色相同的点。在低光环境下,我们会把更多的颜色辨识为“红色”或“绿色”,而无法分辨橙色和黄绿色的细微差别,这和我们的预期相符。
当我们在暗室里观察简单的测试图像时,可以看到这种颜色偏移。然而,在观看真实场景时,我们感知到的颜色并不随光照强度而变化。正如引言部分提到的,颜色恒常性(color consistency)能够将我们的感知恢复为已知应该存在的颜色。我们无法将很暗的橙色视为橙色,但如果它过渡到一种我们能够识别的较亮的橙色,我们的视觉系统会自动判定这两者为相同颜色。
我们的中心视觉(central vision)缺乏对短波长敏感的 S 视锥细胞,并且覆盖着黄色色素。而周边视觉(peripheral vision)有三种类型的视锥细胞,且不含黄色色素,因此与中心视觉的颜色感知不匹配。不过,我们的眼睛和大脑能够在很大程度上自动校正这种差异,就像处理视觉“盲点”一样。我们稍后会展开讨论这个话题。
除了视锥细胞和视杆细胞之外,人眼还有第五种类型的可以探测光线的细胞。先天遗传性失明、没有视杆和视锥细胞的小鼠,仍然拥有瞳孔随光照强度变化而扩张和收缩的反射行为,也依然可以感受到昼夜的变化。这说明,即使我们已知的所有探测器都不存在,仍然有某种机制能探测到光照强度,这就是内在光敏性视网膜神经节细胞(intrinsically photosensitive retinal ganglion cells)的作用。视网膜神经节是位于视杆细胞和视锥细胞旁边的神经束(tangle of nerves),主要负责处理基本的颜色和边缘信息。这些细胞中的一部分也也可以探测到光线。尽管它们的敏感度不高,数量也不足以单独形成用于生成清晰图像的第四条通道,但它们可能以其他方式影响着我们的视觉感知。比如,它们可能影响我们对白色的整体感觉,或以其他方式微调视网膜神经节的颜色处理,同时也参与控制瞳孔的反应。它们对 460~484 纳米范围内的光最为敏感。
对高饱和度或高亮度的颜色而言,还存在其他非线性效应。在高光照水平下,耀眼的高光会产生视觉后像(after-images);在低光照水平下则有浦肯野效应,但它只在视杆细胞适应了低光照水平之后才会发生,这个适应过程需要数分钟时间。这些随时间变化的效应很难预测,幸运的是我们通常能够意识到它们的存在,并且认识到它们是“不真实的”。
三色近似理论在正常色觉下是成立的。对于超出正常色觉的很暗或很亮的颜色,我们的视觉依然尽力保持颜色恒常性,并且试图主动补全那些应该存在的颜色。虽然模型和简单实验可以预测颜色的偏移,但在观看真实场景时,这种预测的偏移并不总是会出现。我们采用三色理论解释正常色觉,是因为它在多数情况下十分有效;我们对异常色觉同样使用三色理论,是因为没有找到更好的解释方法。这可能也反映了我们的视觉皮层在处理色觉时采用的相似机制。
阿布尼效应(The Abney Effect)
下面是一个高饱和颜色的非线性效应的实例。取一个非常饱和的、接近于单色的颜色,将其与白色混合,混合后的色相(hue)还能保持吗?
1909 年,阿布尼爵士(Sir William de Wiveleslie Abney,1843-1920)对这个问题进行了相关研究。他使用了一种白色和一种彩色光源,以不同比例将两种光源射入两根矩形玻璃棒,玻璃棒另一端带有光学扩散片(diffuser)。光线在玻璃棒内随机反射和散射,最终在出口处形成了一个均匀的色块。他发现,当添加白光时,色块的色相(hue)会发生变化。这种现象称为阿布尼效应。
下图是我制作的一个用于研究饱和色彩的装置。如图所示,装置的盖子已经被取下。我使用了一台便宜的的数字投影机,移除了色轮,使其能够投射黑白图像。我将其对准一个分级的二色性滤光片(graded dichroic filter),通过改变发送至投影机的图像,在两个玻璃棒的末端生成了两种独立的自定义光谱。

接下来的光学设置类似于阿布尼的实验装置。每种光谱分别进入一根矩形玻璃棒中,在另一端产生一个均匀的矩形色块。我们需要在昏暗的房间里比较这个正方形色块左右两半的颜色。在这张图片显示的色块中,可以看到左边是蓝色,右边是蓝绿色。
投影机使用的光源是汞灯,其光谱并非在所有波长都均匀。为了校正这一点,我对生成投影图像的软件进行了校准。虽然色块亮度(brightness)受到汞灯光谱的限制,但它发出的光足够明亮,可以模拟我当时正在研究的投影胶片的颜色。由于分色镜的限制,波长分辨率约为 8 纳米,黑色区域并非绝对黑暗,但整个装置已足够好,能够合理模拟出近乎单色光(near-monochromatic lights)的视觉效果。
我观察到了什么呢?对于非常饱和的颜色,其色相(hue)很难判断。我能感受到一些色相的变化,但在缺乏白色参照物的昏暗环境中,很难确定色相是否实际匹配。可以类比一下,在没有足够参照的情况下,被要求挑选一种颜色样本来匹配钠灯光源的颜色,情况大致相似。
以下是由五位作者对阿布尼效应的测量结果,原始图表见:Pridmore RW, Melgosa M (2015) All Effects of Psychophysical Variables on Color Attributes: A Classification System. PLOS ONE 10(4): e0119024. https://doi.org/10.1371/journal.pone.0119024 我将其复制在这里,并感谢作者们的付出,因为完成这项工作无疑需要巨大的努力。
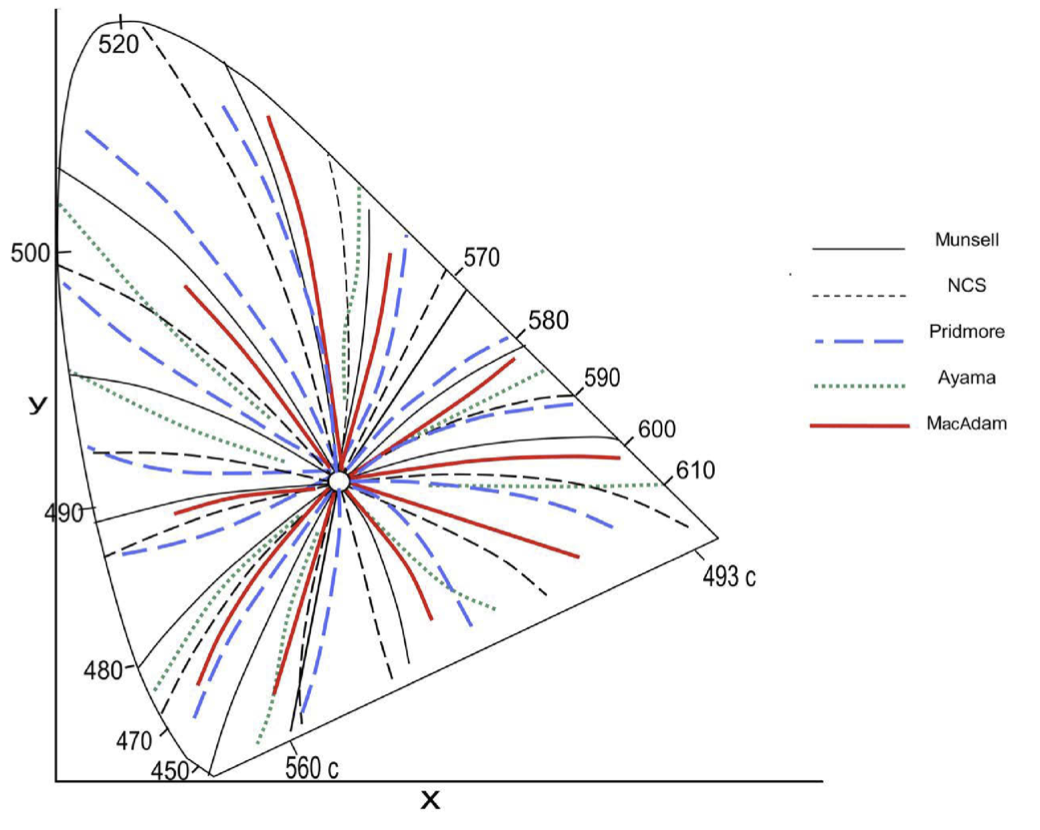
图中的白点位于中间的圆圈处。如果不存在阿布尼效应,则恒定色相感知线应该是从白点向外辐射的直线。
在白点处,LMS 信号接近,因此色相线看起来是直的。越靠近光谱轨迹,非线性效应就变得越明显,导致色相线产生弯曲。如果其中一个 LMS 信号明显大于其他两个信号,或者两个信号大致相同时,你可能会下意识地期望色相保持恒定,因此在红、绿、蓝三基色(primaries)及黄、品、青三种次级颜色(secondaries)处,也能看到近似直线的路径。在研究人员能够直接测量 LMS 基色之前,这样的线索很有价值。
我们能否针对图像的阿布尼效应进行校正?我对这种尝试表示犹豫。图中所示的五位研究人员测量的对象各不相同。观察者之间光谱敏感度的微小差异,在光谱轨迹附近处会变得更加明显。任何相机都有自己的基色和非线性过程,因此也应该有自己的与阿布尼效应类似的效应。
我们是否能在真实场景中观察到阿布尼效应?我认为我们不太可能清楚地看到它。颜色恒常性可以很好地处理反射光颜色的变化,但难以处理这些极度饱和的颜色。这些颜色给人一种自身在发光的错觉,使人感觉光源似乎来自其他地方。个人而言,我更倾向于遵循三色假设,并假定色相线为直线。这种方法简单直接,与那些能够提供良好结果的视觉模型保持一致。至于是否要调整图像使红色更加突出,那取决于个人选择,但我不会将其描述为对阿布尼效应的校正。
CIE 2006 LMS 2 度标准观察者
人眼有三种类型的视锥细胞传感器,分别命名为 L、M、S,它们分别对长、中、短波长的光最为敏感。
通过使用计算机稳定的眼底显微镜(computer-stabilised fundus microscope),我们可以对活体眼中的单个细胞进行成像。在将视网膜曝光并使细胞褪色(bleach)前后,我们可以测定眼内反射光的变化,并根据颜色变化将视锥细胞辨认为 L、M 或 S 类型。我们还可以估计每种细胞对光的最大吸收率。
从活体视网膜上获得高质量的光谱数据是很困难的,但所有的视杆细胞和视锥细胞都通过相同的褪色机制来感知光线。视杆细胞的视紫红质在视网膜死亡后不会褪色,我们可以从中获得较为准确的数据,此外还可以对从视锥细胞获得的噪声数据进行平滑曲线拟合。Lamb 在 Gegenfurtner 和 Sharpe 合著的《颜色视觉》一书第三章中详细介绍了这一过程,以及他用来拟合数据的模型。
以下展示的是一个关于 LMS 敏感度的平滑曲线图。
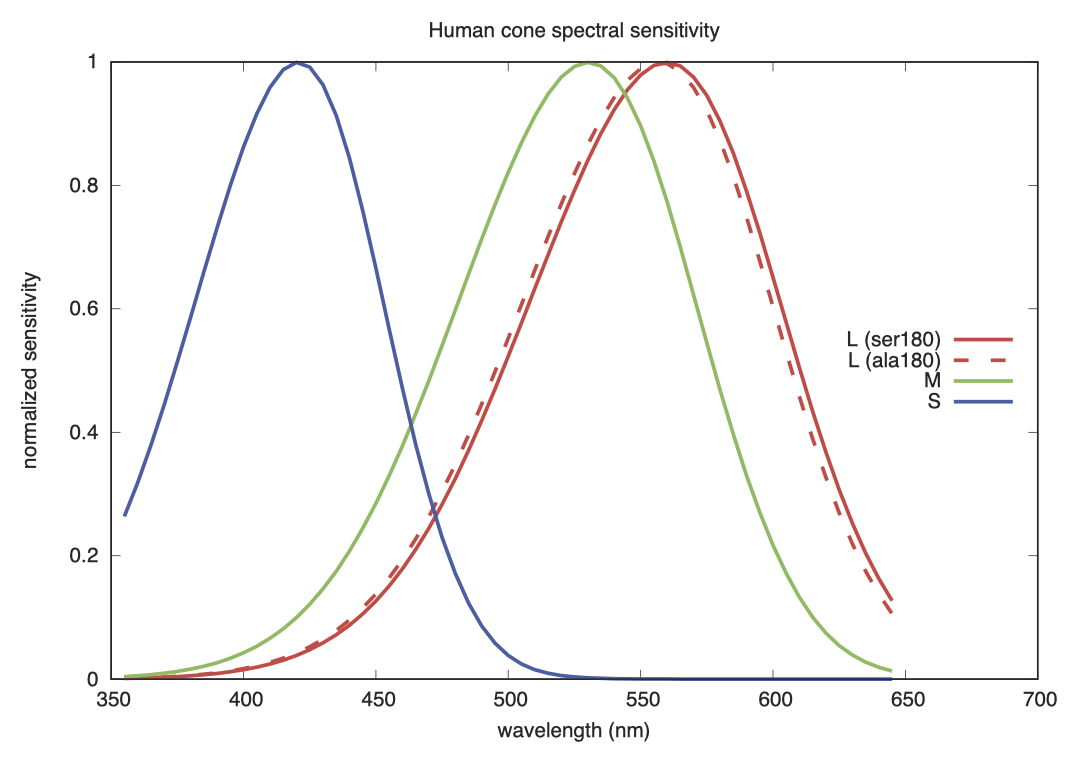
L 视锥细胞色素存在两种遗传变体。约 56% 的测试对象的第 180 号密码子为丝氨酸,其他 44% 则为丙氨酸,这种基因差异使敏感度峰值出现了约 2.7 纳米的偏移。尽管 M 视锥细胞和 S 视锥细胞也存在其他遗传变体,但图中这种是最常见的,也是被研究最深入的。
我们并没有因此采用两套标准观察者。实际上,这两种红色敏感度之间的差异,比这些经过数据清洗的图表所呈现的要复杂得多。最近,Stockman 和 Sharpe 针对 CIE 2006 标准观察者的基色模型,使用了这两种测量结果的加权平均值,以更准确地反映 LMS 原色。
以上结果给出了人眼内细胞对光的敏感度。此外我们还了解到,人眼中的其他光学组件是黄色的,而不是完全透明的。
下图显示了正常人眼晶状体(lens)和黄斑(macula)色素,在低、中、高密度下的光谱透射率函数。横轴为波长,纵轴为归一化的光谱透射率,晶状体为红色曲线,黄斑为黑色曲线。
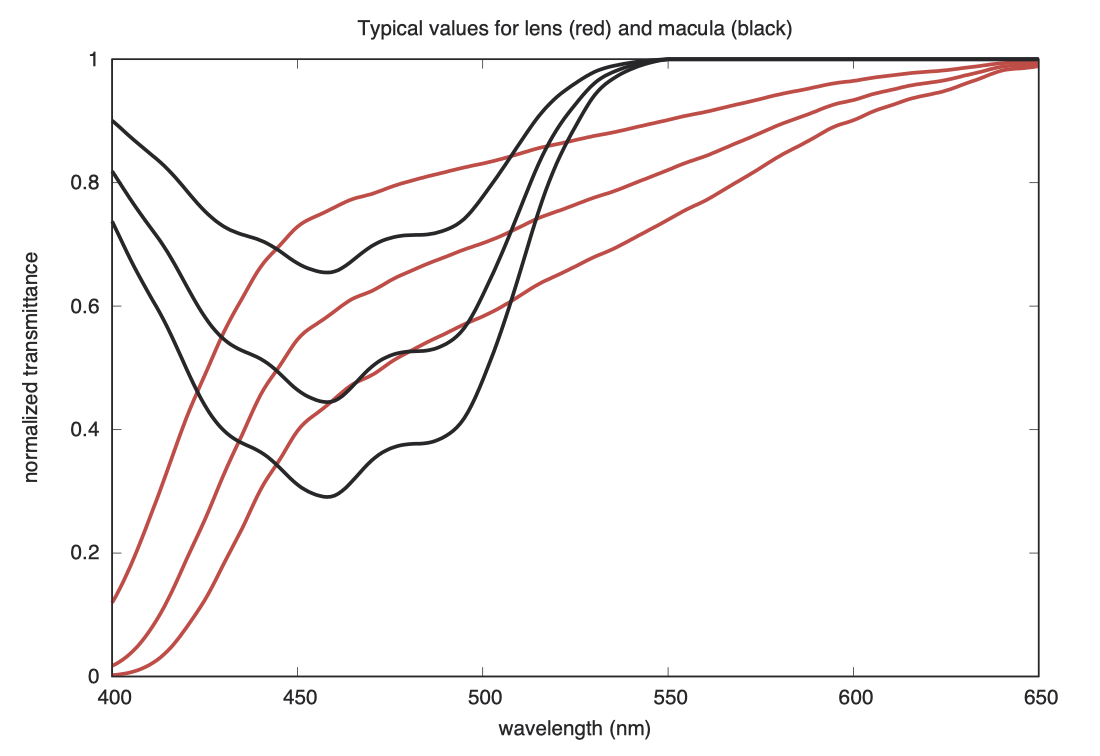
下图是这些晶状体的黄色色素(从上到下)与黄斑的黄色色素(从左到右)可能的组合效果。为了避免黄色超出视频显示范围,图中的背景被设置为灰色,代表透明的晶状体和黄斑状态。

如果我们将视锥细胞的敏感度与晶状体和黄斑色素的平均光谱透射率结合起来,并归一到 1.0,就可以得到 CIE 2006 标准观察者的权值(weights),如下图所示。
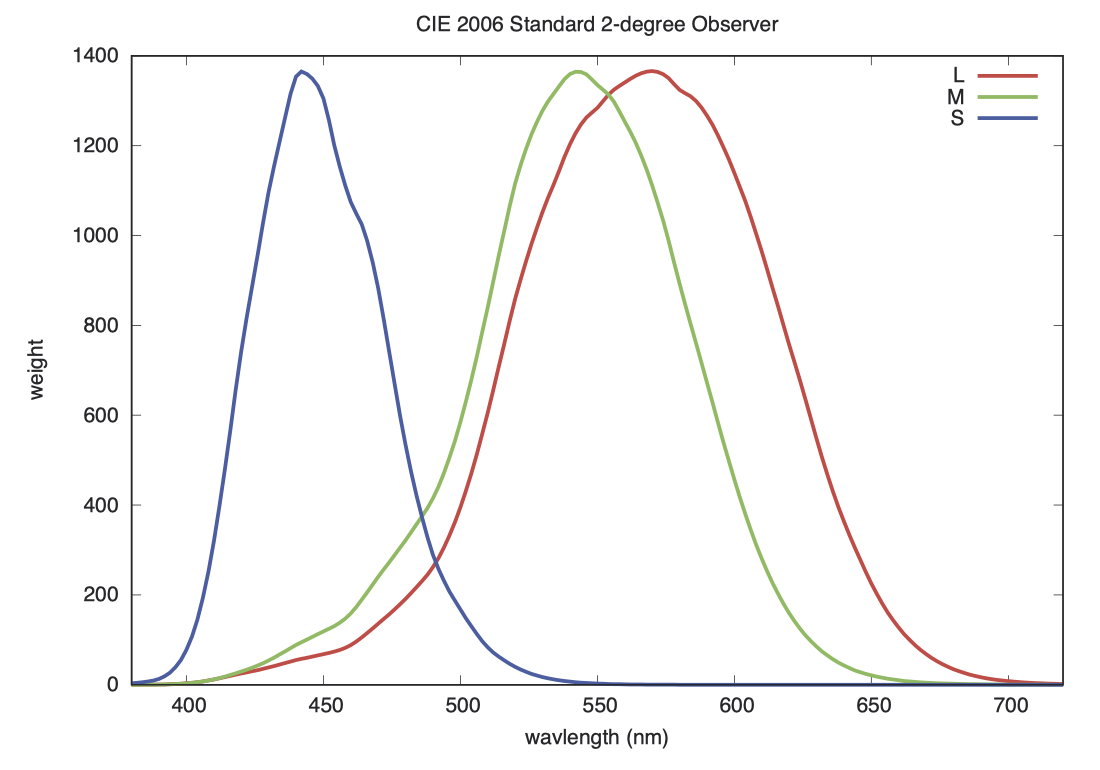
蓝色峰值右侧区域的小凸起,是由黄斑染料的光谱特性引起的。
如果把每种颜色的光谱值乘以相应的 LMS 权值,并把所有波长的值相加,就可以得到该颜色在视网膜上对三种 LMS 视锥细胞的刺激值。如果两种颜色的光谱引发的 LMS 总刺激值相等,则根据标准观察者模型,这两种颜色在视觉上应该是匹配(match)的。这种匹配对于视觉正常的人来说是成立的。
实际上,LMS 基色并不代表真实存在的颜色。比如,没有一种光谱能够仅刺激 M 细胞,L 和 S 总是会同时受到刺激。可以把 LMS 想象成一台与人眼视觉相匹配的摄影机捕捉到的 RGB 值。
CIE 2006 模型的光亮度(luminance) Y 值是由下式给出的。
我们在下一节会讨论什么是光亮度(luminance),以及亮度的来源。
CIE 1931 XYZ 2 度标准观察者
这是一个源远流长的标准。早在 1931 年,人们还无法直接观察或测量视锥细胞中的色素,因此他们通过研究眼睛能观察到的现象来描述眼睛的特征,并得出 XYZ 三个值用于描述颜色。我们首先讨论中间的 Y 值,因为它基于最为简单的实验原理。
Y 值代表的是光亮度(luminance)。我们可以把光亮度(luminance)看做是对明度(lightness)或视亮度(brightness)的测量,但它实际上是通过 闪烁光度法(flicker photometry)[4] 来定义的。我们的眼睛能感受到每秒最多 20 次的光亮度(luminance)变化。但对颜色而言,在两种具有相同光亮度(luminance)的颜色之间进行切换,当闪烁超过每秒约 5 次时,我们就感受不到了。研究者测量了在不同光强条件下,当他们以某个特定频率(例如每秒 10 次)在单色光和参考光之间切换时,观察不到闪烁现象的光强水平。这种实验方法不适合癫痫患者,在研究中也不常使用,但它确实为所有可见波长的光亮度(luminance)权值提供了可靠的实验依据。测量结果与下图中的绿色 Y 曲线相符,可以看到这条曲线在 555 纳米的黄绿色区域处达到峰值,这也是我们视觉感知最敏锐的颜色。因此,这表明 Y 信号不仅反映了我们在 20 Hz 频闪下的视觉感知,而且也与我们通常所说的 视亮度(brightness) 十分匹配。
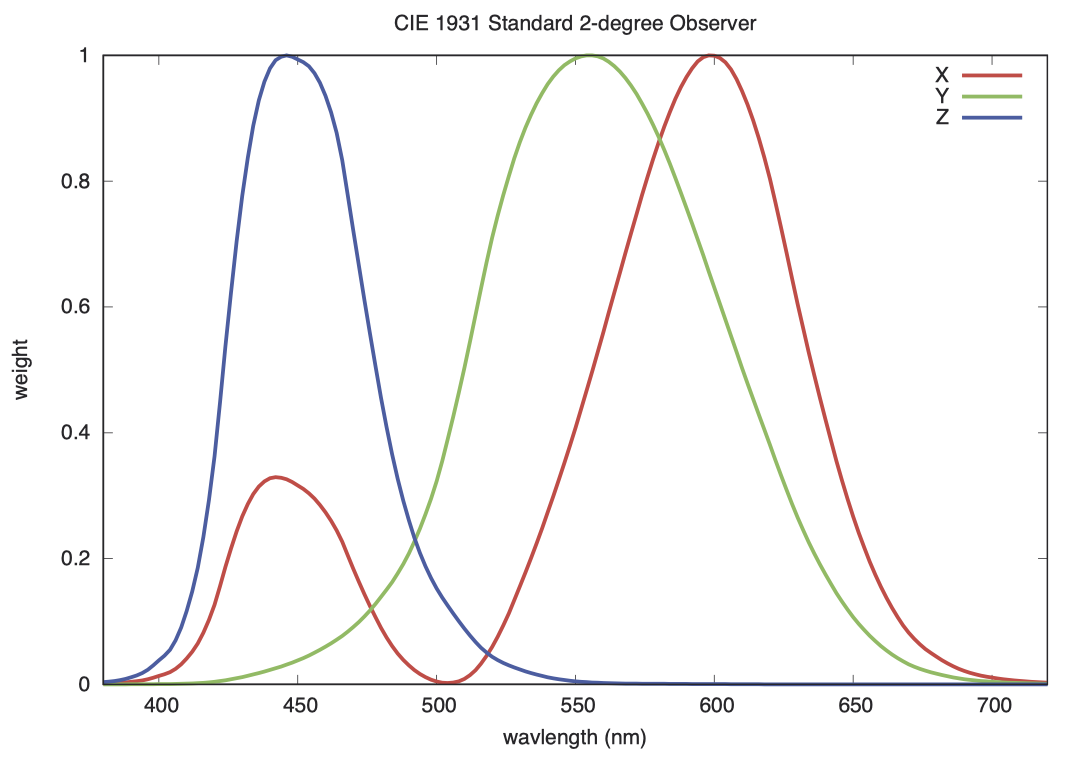
在介绍三色近似理论时,我们考虑了由 650 纳米红光、530 纳米绿光和 460 纳米蓝光混合而成的颜色三角形。这个三角形中并不包含所有可能存在的高饱和度、高亮度(full saturation and luminance)颜色,但确实包含了所有我们已命名的颜色。1931 年标准中的初始研究人员并没有良好的单色光源,但他们通过在白光前增加红、绿、蓝滤光片实现了类似的效果。
假设研究人员将 500 纳米的天蓝色(azure)波长作为目标颜色来匹配。他们可以用 RGB 基色来匹配色相,但无法达到对应的饱和度。因此,对于这类颜色,他们在目标色上添加了一定的白光以降低其饱和度,这样就可以用 RGB 基色来实现视觉匹配了。随后他们从混色中减去添加的白色,得到等效 RGB 值,由此就得到一个包含负值的 RGB 组合,负值代表了位于 RGB 基色三角形外的颜色。
经过多次这样的颜色匹配实验,研究者们建立了一套 XYZ 权值体系。正如根据 CIE 2006 标准计算 LMS 视锥细胞的刺激量一样,我们同样能够计算出光谱的 CIE 1931 XYZ 值。如果两种颜色能产生相同的 XYZ 值,那么这两种颜色就应该是匹配的。
需要注意的是,1931 XYZ 权值与 2006 LMS 权值是不同的。标准制定者明白,他们所确定的 XYZ 值可能并不是人眼的实际基色。事实上,XYZ 权值的任何线性组合都能产生三个数值,对于相一致的颜色能够达成匹配。因为当时无法确定人眼的实际基色是什么,所以他们选择了所能构造的最锐利的函数(sharpest function)的权值。
XYZ 是 LMS 基色的线性组合吗?二者应该是接近的,但实际上有差异,因为 XYZ 是基于更早期、更间接的测量方式得到的。但它们的差异并不明显,否则 1931 年的标准就不会至今仍被广泛使用。许多研究者为了与 1931 年以来累积的文献中大量的测量数据保持一致,只能选择忍受 1931 模型的微小误差。目前,很多测量仪器仍然直接输出 CIE 1931 XYZ 值。
CIE 于 2006 年推出了新的 XYZ 标准,该标准是 CIE 2006 LMS 的线性组合,与旧的 XYZ 标准不同。如果缺乏原始光谱数据,就无法将 CIE 1931 XYZ 数据精确转换为 CIE 2006 LMS。如果你正在处理历史数据,可能仍需使用 CIE 1931 XYZ 标准。如果你在进行新的研究,我建议尽可能使用 2006 年的新标准。无论用哪种方法,都应该尽量保留所有光谱数据。
以下是一个 XYZ 到 LMS 的矩阵转换。这不是从 1931 XYZ 到 2006 LMS 的转换,而是 CIE 2006 标准的一部分,通常作为逆矩阵使用,目的是生成一组尽可能接近 1931 XYZ 标准的基色值。
对于那些不太了解矩阵乘法的朋友来说,这里有一个简化的解释:将矩阵中每一行的数值分别乘以 XYZ 矩阵对应列的数值,然后将乘积相加,由此得到该行的输出值。以最下面一行为例,
在第六章中,我们拟合了另一个矩阵:
最下面一行的数值并不包含我们可能预期的零值。实际上,这行数据是根据 D65 标准白光下的光谱反射率进行平滑处理后拟合的,目的是为了在特定的光照条件下提供更准确的结果。
10 度标准观察者
到了 1950 年代,研究者们清楚地意识到,虽然中心视觉贡献了大部分视觉感知,但周边视觉同样不可忽视。视网膜外侧拥有更多的 S 视锥细胞,不含黄斑色素,而且光线射入视锥细胞的角度也与中心不同(Stiles-Crawford 效应 [5])。这意味着我们的周边视觉与中心视觉对不同波长光的敏感度略有不同。虽然周边视觉并不直接影响中心视觉的反应,但可能影响我们对于白点的整体感知,进而影响我们对颜色的理解。
基于这一认识,研究人员用 10 度视场重复了 2 度视场的视觉匹配实验,并将结果发布为 CIE 1964 10 度标准观察者。
我曾尝试使用 10 度标准观察者进行色彩观测,这个过程比想象中要复杂。当你试图盯着 10 度观测目标的中心时,由于中心视觉区域实际上并没有内容,你必须努力克服不自觉地让眼睛向两侧移动的冲动。如果你能做到目光保持足够静止,你会注意到周边视觉开始逐渐消失(Troxler 效应 [6])。尽管如此,10 度观察者标准还是诞生了,它在预测我们刷墙时看到的颜色,以及对其他包围我们的大面积颜色的感知方面更有优势,但并不是经常被采用。
在使用显示器时,周边视觉的作用尤为显著。在我们第一次同时使用液晶显示器(LCD)与阴极射线管显示器(CRT)进行电影调色时,这一点十分明显。我们用飞利浦探头(一种色度计 colorimeter)将两台显示器的白点校准为视频标准的 D65 白。当我们退后一步,观察两个显示器显示的全屏白色时,LCD 相比 CRT 总是显得略带橙色。我们用光谱仪(spectrometer)重新进行了校准,其结果与飞利浦探头一致,表明这并非仪器读数出错。问题在于,我们是从正常观看距离观察全屏白色的,因此 10 度标准观察者在这种情况下比常规的 2 度观察者更加适用。如果两个显示器都只显示一小块白色区域,则可能察觉不到差异。当显示同一幅典型图像时,差异可能也不明显。但当图像中包含大量白色时,这种差异就变得可见了。
我们在 OLED 显示器上也看到了类似的效果。为了探究这种差异,我在一个黑暗的房间里同时放置了一台 LaCie 的 CRT 显示器和一台索尼的 OLED 显示器,邀请一些观察者坐在舒适的观看距离下,调整 OLED 的显示效果,直到其显示的全屏白色与 CRT 相匹配。随后,我在他们观察的位置用光谱仪测量了两个显示器的颜色。
下图显示了 31 位观察者的观察结果在 CIE u’v’ 色彩空间中的分布。即使忽略个别的离群数据点(虽然我认为这些数据都反映了真实的观察结果),数据点的分散程度与整体的偏移量依然十分显著。这个结果与观察者的年龄没有明显的相关性,这意味着晶状体的黄色色素可能并非重要影响因素。我倾向于认为,黄斑色素的密度在不同观察者之间存在区别,可能是造成感知差异的原因。
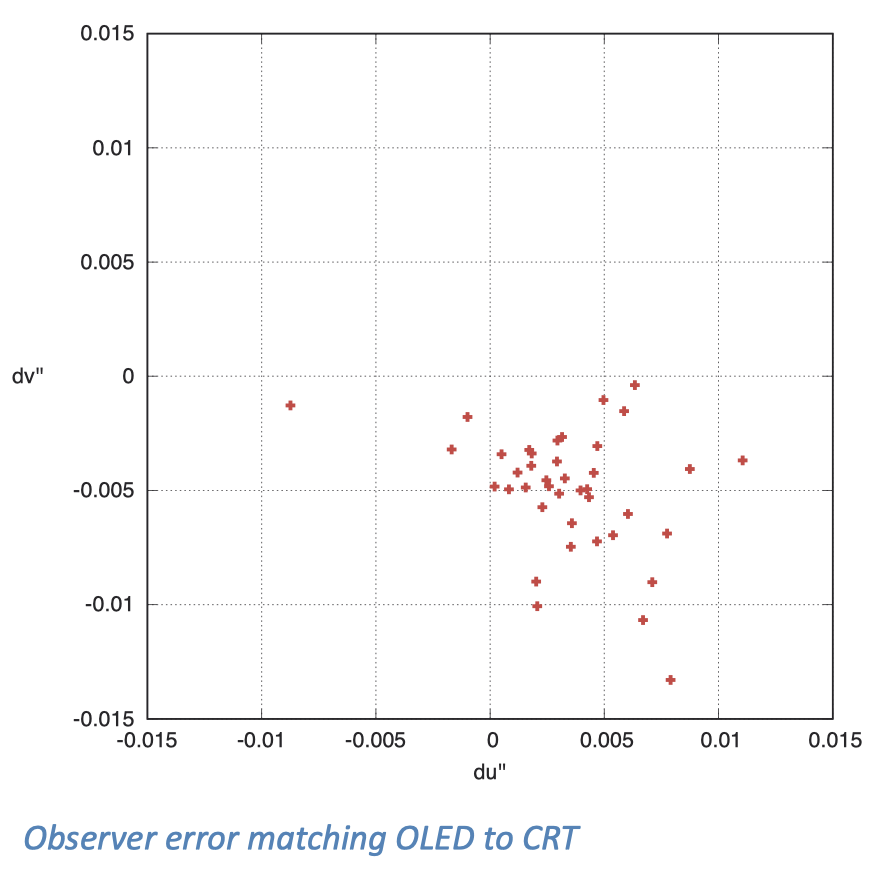
当我们尝试对三色近似理论进行改进的时候,这样的挑战经常发生。特别是在尝试调整适合 10 度视角的观察者模型时,我发现需要对不同个体进行不同的调整。对造成这种情况的原因,我有一些合理的假设,但对解决问题没有什么实质帮助。因此,我最终决定还是使用更传统的 2 度观察者模型,尽管它可能没法完美匹配那些含有大量白色的大尺寸图像。
在另一项实验中,我只使用了 OLED 显示器,并在其中一侧加上了 Roscolux 彩色滤镜,以此改变显示器的基色。这次实验因为保持了像素的一致性而更为准确,但由于光谱的变化幅度较小,所以更难测量。不过,实验结果与之前大致相同:不同的观察者对颜色的匹配存在差异。
我经历过的关于 10 度观察者的最具戏剧性的例子,是在试图匹配胶片与数字投影机的颜色时发生的。我们使用一台索尼氙灯光源 4K 数字投影机作为基础,使用另一台氙灯光源幻灯机在同一个屏幕上投射出匹配的胶片图像。虽然我用测试仪器匹配了两台设备的白点,但我的眼睛总是能看出颜色差异。无论如何手动调整索尼投影机的白点,都无法得到让我满意的匹配。最后,我不再放映图像,而是只观察全屏的白色画面,并调整了数字投影机的白色,使其与幻灯机相匹配。这时,我注意到一个大约 2 度宽的、随眼球移动的、颜色不匹配的斑点,在数字投影机一侧呈现黄蓝色,在胶片幻灯机一侧则呈现淡紫色。这就是所谓的麦克斯韦斑(Maxwell’s Spot)[7]。这一现象证明,数字投影机的白色与幻灯机的白色是不一样的,前者对氙灯光源做了过滤,仅使用了红、绿、蓝三个波段,没有使用中间的波长。
上述经验表明,在 10 度观察者模型下,我们不能只用三种基色来进行颜色匹配,因为我们无法同时匹配中央视觉和周边视觉的白色感知。对于能否采用第四种基色来匹配,我也表示怀疑。每个观察者的匹配的结果都是不同的,而且取决于一个人在特定瞬间的观察位置。我希望大家了解的是,这是三色近似理论中的另一个较小的缺陷,在实际图像中很少看到;应该尽量避免把采用不同基色的显示器放在一起;最后,我们继续使用 2 度标准观察者。
光的单位
在第一章中,我简要地提到了 坎德拉 的国际单位制定义,该定义是罕见的基于频率(540 THz)表示颜色的例子。虽然我们已经探讨了光谱的测量,但对实际使用的测量单位却一笔带过。随着我们对光亮度(即 CIE XYZ 中的 Y)有了更深入的理解,现在可以探讨一下相关的测量单位了。
弧度(rad)是平面角的计量单位,定义为圆弧长度与圆的半径之比。弧度与角度(degree)类似,但在二维平面上的任何一点周围的弧度都是 2 π,而不是 360 度。短弧线可以近似于直线:一条位于 1 米外的、垂直于视线的 1 cm 长的弧线,所对的的平面角约为 0.01 弧度。物体在人眼处所对的角度,决定了物体看起来有多宽或多高。
球面度(sr)是立体角的的计量单位,是球面上一小块区域的面积与球的半径之比。一小块球面可以近似于平面:一个位于 1 米外的、垂直于视线的、边长 1 cm 的正方形平面,所对的立体角约为 0.0001 球面度。在三维空间的任何一点处周围的立体角都是 4 π。物体在人眼处所对的立体角,决定了物体看起来有多大。
坎德拉(cd)的定义是:辐射强度为 1/683 瓦特/球面度的光源,在发出 555 纳米(540 THz)单色辐射时所对应的亮度(brightness)。555 纳米是上一节中 Y 曲线的峰值,我们用这个 Y 曲线来校正其他波长。例如,510 纳米光的权值为 0.503,我们对它的敏感度大约是 555 纳米的一半。我们看不到红外线或紫外线,因此它们的权值为 0。
引入 1/683 这一常数,是为了让坎德拉的定义能够与早期基于戊烷灯的标准保持一致,而并非基于蜡烛,这是一个常见的误解。
在下图中,第一个正方形的面积为 1 个单位,到光源的距离为 4 个单位。使用小球面的近似计算可得,第一个正方形所对的的立体角约为 1/16 球面度。第二个正方形的面积是它的 4 倍,到光源的距离是它的 2 倍,所以它所对的立体角也约为 1/16 球面度。等量的光(以瓦为单位)散布的区域更大了,但以坎德拉度量的亮度(brightness)是一样的。
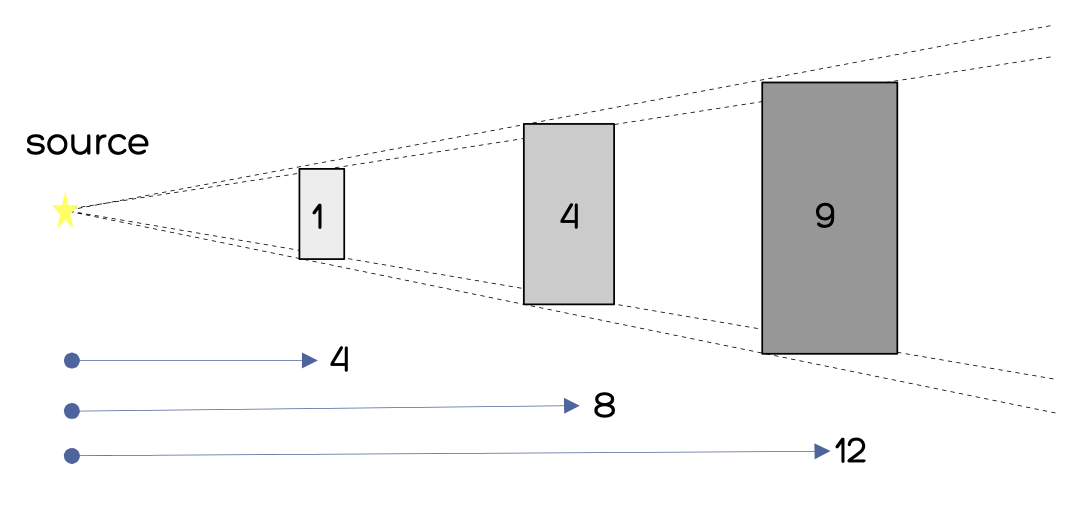
坎德拉度量的是光源在一个立体角单位内的光输出总量。对于像平板显示器这样较大面积的光源,我们通常会用坎德拉/平方米(cd/m ²)或尼特(nit)表示单位面积的亮度(brightness),后者来自拉丁文的“nitere,意为“闪耀”。尼特并非一个国际单位制术语,但因为其使用广泛且方便打字录入,所以从下文开始我将使用 nit 代替 cd/m ²。一个典型的计算机显示器的亮度约为 100~400 nit。
1 英尺朗伯(ft-L)是 3.426 nit。尽管在 2000 年的美国这一单位还相对常用,但如今已较为罕见,仅在一些旧的标准文档中还能看到。电影院的片门全开的白色标准是 16 ft-L。
特罗兰(troland,td)是亮度(brightness,nit)与瞳孔面积(mm²)的比值。这是一个度量视网膜曝光量的单位,其中增加了瞳孔大小的校正因子。瞳孔面积可以是实际人眼的测量值,也可以是放在眼睛前面的小型人造瞳孔的面积值。这个单位主要出现在研究论文中,平时接触的机会不多。在本书中有一张图表的纵轴采用了特罗兰作为单位。在一个标准的 10 mm ² 瞳孔面积下,10 td = 1 nit。
我们用 流明(lm)表示总的光输出,它是亮度(brightness,cd)与立体角(sr)的乘积。这种度量方式特别适用于发出近似平行光的设备(如激光),因为在这种情况下,光束的立体角基本可以忽略不计。一台小型数字投影机的光输出可达几千流明(Klm)。在投影机变焦或调焦时,其发出的用 lm 衡量的总光量应该基本保持不变。
照度(illumination)的国际标准单位是 勒克斯(lux,lx)。被光均匀照射的物体,在 1 ㎡ 面积上获得的光通量是 1 lm 时,其照度为 1 lx。明亮的室内照明约为 1000 lx,而 1 lx 则适用于需要较暗光照的环境,如演讲厅(lecture theatres)和胶片电子转录室(telecine suites)。
朗伯反射体(Lambertian reflector)是一个完全的漫反射体,能够向各个方向均匀反射光线。如果有一个表面是完美白色的朗伯反射体,则它在 1 lx 的光照下,反射的光亮度应该等于 1/π nit。
现代测色仪器
在上文中我们已经提到了分光镜(spectroscope)。以下还列出了我们可能遇到的不同的测色仪器。
分光镜(spectroscope)一般不直接用于颜色测量,因为它们没有配备探测器。使用者需要通过肉眼观看光谱线和其他特征。不过,可以在分光镜上安装一台相机来进行曝光测量。而那种可以测量每个波长的光线强度的设备,一般称为光谱仪(spectrometer),见下文。
测光表(light meter)可以测量来自某个光线探测器的信号,其读数是以曝光量单位给出的。
测辐射热计(bolometer)或 辐射计(radiometer)或 辐照度计(irradiance meter),测量的是每秒钟落在传感器上的辐射量。这类仪器经过校准后,可以显示以瓦特(W)为单位的总功率;如果考虑探测器的表面积,则单位为瓦特每平方米(W/m ²)。这些设备可能配有滤光片,用于限制它们可探测的特定波长范围,从而能够专门测量红外线、紫外线或可见光。
照度计(lux meter)是一种带有滤光片的测光表(light meter),其光谱灵敏度与人类视觉亮度(human vision luminance)相匹配。它可以测量以勒克斯(lx)为单位的漫反射光,也能测量以尼特(nit)为单位的相干光(coherent light)[8]。以勒克斯为单位的仪器通常会有一个白色的漫反射球,可以收集来自已知区域内所有方向的光线。以 nit 为单位的仪器通常会有光学装置或准直(collimation)装置,用于控制其测量光线的立体角。
色度计(colorimeter)与辐射计(radiometer)类似,但配备了三个传感器,其上通常分别装有红、绿、蓝三种滤光片,以模拟人眼对颜色的反应。这些仪器是测量宽频光(broadband light)的经济有效的方案,也适合测量一些特殊的设备,如配备标准荧光粉的视频监视器。不过,它们不适合测量光谱,特别是当光谱中存在与红、绿、蓝三色敏感区域的边缘重叠的尖锐波段时。装有大型探测器的色度计可以做到对光线极为敏感。事实上,大多数现代数字彩色摄影机也可以看作是由众多色度计组成的阵列。
密度计(densitometer)相当于一个自带光源的色度计(colorimeter),有些用于测量透射光,有些用于测量反射光。它们以对数单位的密度值给出针对待测光的测量结果。密度为 0.0 的物体能够透射或反射所有的光,密度为 1.0 的物体能够透射或反射 1/10 的光,密度为 2.0 的物体能够透射或反射 1/100 的光,依此类推。彩色密度计可以使用白光结合红、绿、蓝色滤镜进行测量,这些滤镜的作用是为了与被测物体中的色素相匹配,如测量胶片底片时使用的 Status M 滤镜;或者是为了与人眼的色彩敏感度相匹配,如测量正片时使用的 Status A 滤镜。[9]
光谱仪(spectrometer)则通过将光谱分解为许多小的波长带(wavelength bands)来完成测量。一个典型的固态光谱仪通过狭缝观察光源,并使用光栅(grating)将光源的图像分散到一排探测器上,从而获得光谱信息。这种仪器的灵敏度比色度计(colorimeter)低,因为光线经过了准直(collimated)以获得清晰的光谱,随后再分散到多个探测器上,这可能会限制其测量深色阴影色调(deep shadow tones)的能力。光谱仪可以根据标准光源进行校准,确保在测量每个波长带时都有精确的波长和灵敏度。
光谱仪(spectrometer)在没有配备光学元件的情况下,不适合用于测量工作环境下的色块等对象。用于测量颜色的典型光谱仪,一般会配备一个镜头(lens)和一个目镜(eyepiece),在这种情况下它可以被称为 遥感光谱辐射计(telespectroradiometer)。在目镜中,光谱仪的取样区域会显示为一块暗区。经过校准后,这类仪器可以测量单位为瓦特/平方米·球面度·纳米(W/m ²· sr · 纳米)的光功率。
多光谱相机(multispectral camera)与 RGB 相机类似,但拥有更多的颜色通道。这些相机特别适用于机器视觉、植物健康监测等领域。多光谱相机可以像大多数 RGB 相机那样使用固定的滤光片阵列,也可以使用单色探测器并切换滤光片,以捕捉多种颜色通道的信息。
高光谱相机(hyperspectral camera)的每个像素都能返回一组光谱分布数据。“Hyper”前缀表明它的探测能力超出了人眼可见的光谱范围。这类相机通常能够探测到紫外线和红外线区域,但其具体能力取决于设计和用途。由于能探测的波段很多,传统的滤光片阵列无法满足需求,因此它们采用逐行或逐波段扫描整个图像的方式来捕捉信息。这种技术使得它们在捕捉运动对象时表现不佳,但在卫星遥感、科学研究、早期绘画或彩色胶片等历史图像扫描等领域,具有独特的应用价值。
然而到目前为止,这些仪器都没有告诉我们颜色看起来是什么样的。在下一章中,我们将探讨亮度-色度色彩空间(luminance-chrominance colour spaces)以及感知均匀色彩空间(perceptually uniform colour spaces)。在后者中,相等的间隔对应着相等的可见对比度(equal intervals should correspond to equal visible contrasts)。
- 1.海丁格尔刷效应:1844年,奥地利生理学家威廉·海丁格尔博士(Wilhelm von Haidinger, 1795-1871)通过研究发现:在一定条件下,人眼可以对线偏振光产生感知效应,其主要表现为,因入射人眼的线偏振光偏振角变化所引起的视觉图像强度变化。这种奇妙的视觉效应看起来就像一只黄色领结与一只蓝色领结呈十字交叉,形状如同一个旋转的刷子,是由人眼黄斑对线偏振光的吸收作用而产生的内视现象,所以人眼对偏振光的感知效应也被称为海丁格尔刷效应(Haidinger’s brush)。人们对海丁格尔刷效应图像的光学解释也进行了很多探讨,其中径向偏振片假设是最普遍被接受的理论。根据这一理论假设,海丁格尔刷效应的产生归因于人眼黄斑中的 Henle 纤维层上呈径向对称结构分布的黄斑素,对入射人眼的线偏振光进行了选择性吸收,线偏振光的方位角差异遵循马吕斯定义被转化为黄斑解剖层内的图像的亮度变化,最终在人眼的视野中产生了强度调制图像。所以海丁格尔刷效应的光谱特征与黄斑色素的吸收光谱特征相对应,其灵敏波长主要集中在蓝光波段,于 460 纳米处有清晰的峰值并在 520 纳米处截止。基于这种海丁格尔刷效应图像与人眼黄斑结构的依赖特性,当黄斑变性或视网膜病变等疾病破坏黄斑的径向对称分布结构时,会改变黄斑底层的感光细胞所接收的海丁格尔刷效应图像,导致海丁格尔刷效应图像变化或消失。因此,在医学应用方面,海丁格尔刷效应图像检测可以作为告知患者黄斑结构特性和黄斑色素密度变化的工具,还可以作为包括年龄相关性黄斑变性和糖尿病型视网膜病变等黄斑病变的诊断手段。详见:王祺,刘智颖,贾文涛,黄蕴涵,贺文俊.人眼海丁格尔刷效应的偏振感知建模与分析(特邀)[J].红外与激光工程,2022,51(01):413-421. ↩
- 2.浦肯野位移:又称为浦肯野效应、薄暮现象,于1825年由捷克生理学家浦肯野(Jan Evangelista Purkyně,1787-1869)发现,是人眼峰值亮度敏感性在低照度条件下向蓝色光谱移动的趋势,是暗适应的一部分。其表现为:高明度下,红色比蓝色明度强;低明度下,蓝色比红色明度强。这种效应会在不同照明水平下引入颜色对比的差异,例如,在明亮的阳光下,天竺葵的花朵呈现出明亮的红色,与其叶子的暗绿色或相邻的蓝色花朵形成对比,但在黄昏时观察同一场景时,对比度会反转,红色花瓣会呈现出暗红或黑色,而叶子和蓝色花瓣则相对明亮。该效应体现了暗视觉下视杆细胞中视紫红质的吸收最大值(约为 500 纳米)与明视觉下 L 视锥细胞中视紫蓝质的吸收最大值(约为 555 纳米绿色)之间的关系。该效应是从以感色细胞为主的阶段转变为以感光细胞为主的阶段过程中的一个状态,即当外界光度逐渐降低,视锥细胞活跃状态随之降低,视杆细胞开始接手成为视网膜上主要接受光源的细胞,在辨识颜色能力完全消失之前的这个阶段。 ↩
- 3.特罗兰(Troland,td):视网膜照度单位,td = 刺激亮度(cd/㎡) * 瞳孔面积(mm²)。当光进入眼内到达视网膜,视网膜上被照明区的光照度为视网膜照度。 ↩
- 4.闪烁光度法(flicker photometry):一种用于测量视网膜中视锥细胞的颜色敏感度的技术。这种技术利用了人眼对快速闪烁光的视觉暂留效应,通过比较两个快速交替出现的光源的亮度来测量视网膜中的颜色敏感度。在闪烁光度法中,两个光源交替快速闪烁,一个光源的颜色保持不变,另一个光源的颜色逐渐变化。测试者需要调整两个光源的亮度,使得两个光源看起来相同,这时就可以确定被测颜色的亮度敏感度。闪烁光度法可以用于研究人类和动物的视觉系统,例如研究色盲和色弱症、研究视网膜色素变性症等视网膜疾病,以及研究动物视觉系统中颜色敏感度的进化和适应性。 ↩
- 5.斯泰尔斯-克劳福德效应:由斯泰尔斯(W. S. Stiles)和克劳福德(B. H. Crawford)在1933年发现的现象。通过瞳孔中心的光和通过瞳孔周边的光在视网膜上的同一位置成象,但到达视网膜的角度是不相同的。视锥细胞的敏感度随这一角度而异,即对通过瞳孔中心直射在视网膜上的光敏感度最高,而对于离中心如 4 毫米的周边处入射的光敏感度可减至 1/3 以下。这一现象在中央凹处十分显著,但在视网膜周边区却几乎看不到,因此一般认为在视杆细胞缺乏这一现象。关于引起这种现象的机制有各种学说。有一种学说认为,这一现象是因为沿视锥细胞长轴方向入射的光,在细胞侧壁全反射,未向细胞外逸出而到达视锥细胞外段;但若超过某一角度,入射光将从细胞侧壁逸向细胞外。但也有一种观点认为,中心窝视锥细胞的直径(2微米)与光波长为同一数量级,因而把它看作如微波的波导管那样更为妥当。 ↩
- 6.特克斯勒消逝效应(Troxler's fading):瑞士物理学家特克斯勒于 1804 年发现的效应。他指出,当一个人的目光聚焦在某个固定点上 20 秒或者更长时间之后,在该固定点周围,也就是在观察者余光中的其他视觉刺激源,将会在观察者的视野中慢慢淡化直至最后消失。特克斯勒消逝效应是一种生活中较常见的现象,是神经适应性(adaptation)的表现。神经适应性是指人的感觉系统对外界的持续刺激不是恒定不变的,而是有一种适应刺激的过程。这种适应性使得神经系统可以忽略某些不重要的信息,比如这种持续不变的刺激,进而使人可以更好的应对环境中不断变化的信息。 ↩
- 7.麦克斯韦斑:最早于 1856 年由麦克斯韦在观察蓝光时发现。当一个正常的观察者通过透射红蓝光的二色性滤光片(dichroic filter)观察白色表面时,在视野中心可以看到一个红斑,这种现象被称为麦克斯韦斑,通常解释为由于黄斑色素对蓝光的优先吸收而产生的一种内视现象(entopic phenomenon)。在各种类型的麦克斯韦斑中,最常见的是对称的圆形,由三个同心区组成:一个斑点、一个透明环和一个光环,从中心到外侧排列。中心光斑和外侧光环是红色的,而透明环的色度与背景场相同,在大多数情况下是蓝红色的。该现象是由于黄斑中的叶黄素吸收了更多蓝光导致的。该现象也能够证明有两种颜色匹配函数,即中心视野(2°)的函数和包含周边视觉(10°)的函数。当颜色坐标在周边视觉中实现同色异谱时,在中心视觉中可能不是同色异谱的。 ↩
- 8.相干光:频率相同、振动方向相同、周相相等或周相差恒定的两束光。相干光相互交迭时,可产生稳定的相位差,且合振幅也恒定,能形成稳定的光强分布,形成干涉条纹。激光具有较好的相干性,利用激光的相干性可进行精密测定、微定位、激光陀螺及全息照相等技术。 ↩
- 9.状态密度测定:不经滤色光谱校正的密度计测量结果可以用于不同实验室的密度测试结果比较,这种密度计称为状态密度计(Status Densitometer),测量方法称为状态密度测定法(Status densitomery)。实际工作中,为适应不同胶片的测量,常用许多滤镜与密度计配合使用,常用有两类这样的滤镜系列,分别称为 Status A 密度计和 Status M 密度计。前者用于彩色正片(如反转片、拷贝片)的测量,后者用于彩色印像片(如彩色负片、中间拷贝负片、低反差反转片、反转中间拷贝片等)的测量。这些滤镜系列由一些公司生产,可以从这些公司购买到。胶片的特性曲线一般会注明使用什么密度计测量,比如 E100VS、RVP 等的特性曲线表注明密度计是 Status A。 ↩
转载请注明来源。欢迎留言评论,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。