由 Filmlight 公司的色彩科学专家理查德·柯克(Richard Kirk)撰写的色彩科学白皮书《颜色:感知与测量》(Colour: Sense & Measurement)第二章(翻译初稿)
译者:Horace Lu
原书下载地址
这一章主要讨论测量光线的仪器和技术。我将描述我所看到的颜色,以便将波长的数值与人眼可见的颜色对应起来。本章中还包含了一些关于历史上人们如何命名颜色的记录。不过,关于人类视觉的讨论在本章并不是重点。本章的重点是测量技术,而关于视觉的深入探讨将在第三章展开。
光谱中的颜色
我有一个可调节波长的单色光源,来自我在垃圾堆中翻到的一台旧的珀金埃尔默(PerkinElmer)分光光度计。它的测量模块不能正常运行了,但光源仍然出奇地准确。我可以转动一个旋钮,来获得特定波长的光。以下是我看到的颜色:
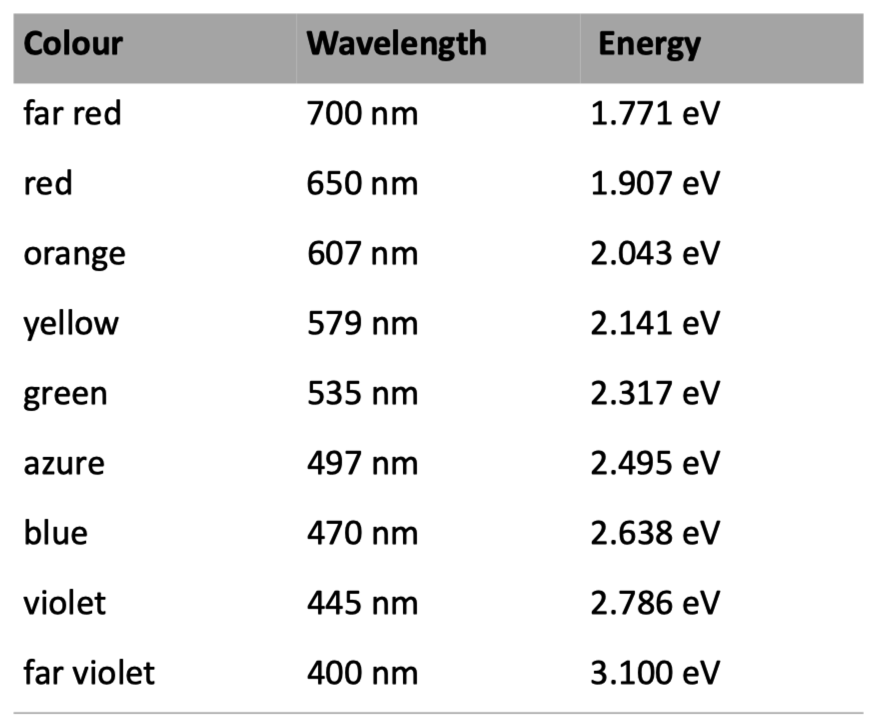
如果你不是物理学专业的,就不必在意这些细节。可见光波长通常以纳米(纳米)为单位,其数值范围大约在 400 到 700 纳米之间。我们也可以用微米或千分之一英寸来表示这些数值。简单来说,每种颜色在光谱中都对应一个特定的数值。
虽然标准波长是在真空中测量的,但我们生活在有空气的环境中。在室温下,可见光在空气中的折射率(refractive index)约为 1.00027,这意味着在真空中波长 500 纳米的光,在空气中的波长大约是 499.86 纳米。空气中光的波长的准确数值还受到气压和温度的影响。幸运的是,波长在空气和真空中的差异非常小,因此我们通常以纳米为单位来表示波长,无需担心光线是在真空中还是空气中,其差异在视觉上是无法察觉的。
上表的最右一列是以电子伏特(eV)为单位的光子能量。这是一种比波长更加精确的测量方式,因为无论是在真空、玻璃、空气还是水中,电子伏特的值都是相同的,它代表单个光子中的能量。例如,典型的碳-碳单键的键能在 3.6 ~ 3.9 eV 之间,这说明紫外线可能对有机化合物造成伤害。另一个很好的测量方式是频率,其在不同介质中的值也是一样的,而且它可以直接关联到七个基本测量单位之一:国际单位制(SI)规定的可见光强度单位坎德拉(cd)最初是基于波长 555 纳米的光定义的,而现在则是基于频率为 540 THz(波长 555.18 纳米)的光来定义的。这是我所知道的唯一一个使用频率来描述光的例子。从下文开始,我们将始终使用纳米作为描述单位。
以下是对我所观察到的一些颜色的记录:
- 在光谱的远红(far red)区域延伸至 700 纳米之外时,颜色变得难以辨认。在我记录为大约 690 纳米的位置,颜色看起来比标准的红色略微偏橙一点。这可能是真实的颜色效果,也可能是由于较短波长的轻微污染,或是由于视网膜对辐射中的热量而非光子做出反应,或是受到其他过程的影响。白炽灯会放射出大量的红外线。安全系统常用的红外 LED 标称波长通常在 900 纳米左右,但仍然会产生可见的红光。
- 红色(red)在 650 纳米及以上的波长范围内保持一致,与深红色(deep red)的 LED 灯颜色相似。
- 橙色(orange)并没有一个明确的定义点。我选择 607 纳米作为典型的橙色。
- 有一条相当清晰的狭窄“黄色(yellow)带”,它的一侧是“金色美味”的绿黄色(green-yellow),另一侧是“黄油般的”橙黄色(orange-yellow)。我将 579 纳米选择为“柠檬”黄。
- 绿色(green)也没有一个明确的定义点,而是存在一个我们称之为绿色的范围。535 纳米是典型的“红绿灯”的绿色,位于这个范围的中间处。
- 有一条明显的“天蓝色(azure)带”,一边是蓝色,一边是绿色。它不像黄色那样精确,但仍然相当独特。为了与其他欧洲语言兼容,我选择将其称之为“天蓝色”。“青色(Cyan)”通常用于描述印刷颜色或显示颜色,但这两种青色不完全相同。
- 没有明显的“蓝色(blue)”点。我选择的“天蓝色(azure)”和“紫色(violet)”的中间点是 470 纳米,这个位置在我看来是一种非常典型的蓝色。
- 从 445 纳米往下,紫色(violet)就与蓝色有明显区别了,更短波长的部分都是明显的紫色。
- 在大约 420 纳米以下,紫色似乎失去了饱和度。能看到的最短波长的紫色是 370 纳米,但遇到了与远红相同的问题:人眼对这些波长不敏感,并且我们看到的颜色可能被其他颜色所污染。我的实验也受到了光源(白炽灯)的限制,因为白炽灯发光的紫色成分很少。
早期的波长测量
托马斯·杨(Thomas Young,1773-1829)是一名训练有素的医生,一生都对医学和解剖学抱有浓厚的兴趣。此外,他还对语言学、象形文字等许多领域感兴趣。1800 年,他在准备一篇关于人类声音的论文时,不仅梳理了声音的基本原理,还延伸到了光与视觉的领域。用他自己的话来说:
当我开始着手撰写关于人类声音的论文的大纲时,我发现自己对声音本质的理解是模糊不清的。在剑桥大学伊曼纽尔学院(Emmanuel College, Cambridge)的三年学习中,我搜集了所有能从书本上获得的相关信息,并针对多种声音以及流体的运动进行了各种原创实验。在研究过程中我惊奇地发现,欧洲大陆的研究者在发声体与弹性流体运动的研究方面,比我们英国的同胞走得更远。在进行有关声音如何产生的实验时,我强烈地感受到,我所观察到的现象与我已经了解的薄膜干涉产生的颜色现象(colours of thin plates)十分相似,这让我开始怀疑它们之间存在着难以置信的紧密联系。
这段话是对托马斯·杨的一个很好的写照。在大学时期,他因非凡的才华而拥有了“奇迹杨”(Phenomenon Young)的绰号。作为一位涉猎广泛的学者,他具有敏锐的洞察力,能够设计出既简单又精确的实验,直观地揭示光学的基本原理。不同于许多前辈天才,他还积极与其他科学家合作,特别是奥古斯丁-让·菲涅尔(Augustine-Jean Fresnel,1788-1827),这一合作在当时英法关系紧张的背景下显得尤为特别。
托马斯·杨首次发表了对不同颜色的光的波长的准确估计。他对颜色的命名,和他给出的光波长数值(以每英寸波长计),以及我转换成纳米的数值如下:
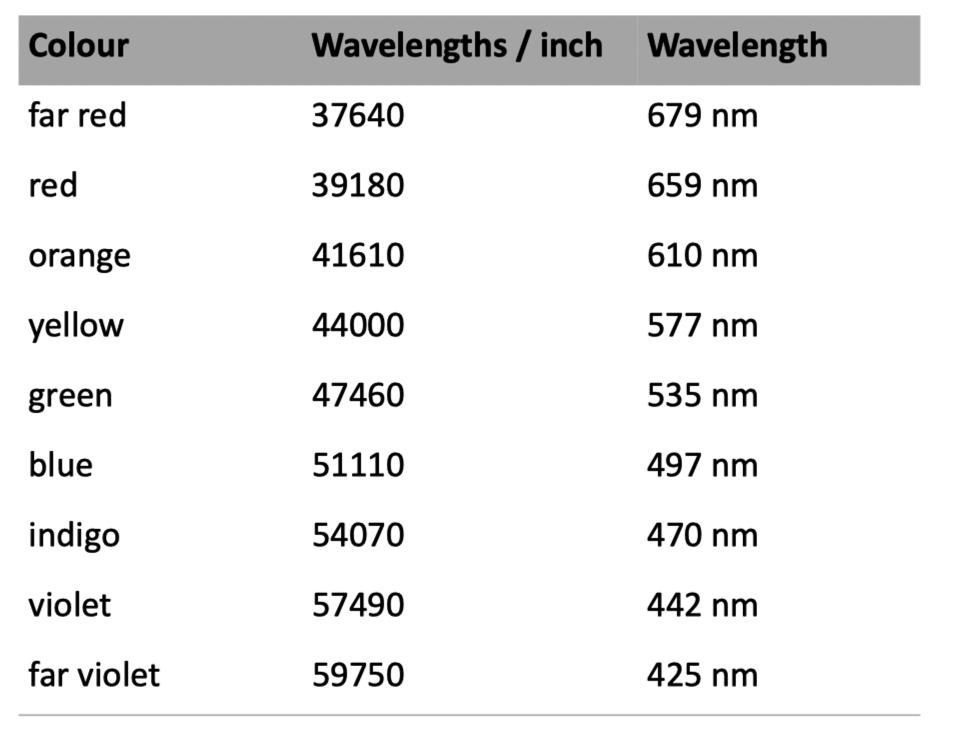
请注意颜色的命名方式。他的“蓝色(blue)”对应我的“天蓝色(azure)”,他的“靛蓝(indigo)”则对应我的“蓝色(blue)”。
艾萨克·牛顿(Isaac Newton,1643-1727)在其 1730 年出版的《光学(Opticks)》的多佛重印本 [1] 第 52 页,列出了来自棱镜的颜色:“紫色(violet)、靛蓝(indigo)、蓝色(blue)、绿色(green)、黄色(yellow)、橙色(orange)、红色(red)”。牛顿之所以加入“靛蓝”,据说是因为他出于数字命理学(numerology)的考虑,想要凑齐七种颜色。牛顿本人可能有神秘主义倾向,但他的《光学》却是一部简明扼要的、用英语而非拉丁语撰写的作品。他确实提出了一个奇特的理论,将颜色与音乐的音阶联系起来,这或许解释了他希望颜色名称能与音乐音阶中的音符相匹配的愿望(在第 12 章亦有提及)。另一种解释是,由于蓝色(他拼写为“blew”)是指类似天空的“天蓝色(azure)”,因此他需要一个新词汇来描述在此之外的颜色。他在 1733 年的笔记中评论道:
那些本身呈现为红色,或使物体呈现为红色的同质光和射线,我称之为制造红色的(Rubrifick or Red-making);那些使物体呈现为黄色、绿色、蓝色、紫色的光线,我分别称之为制造黄色的(Yellow-making)、制造绿色的(Green-making)、制造蓝色的(Blue-making)、制造紫色的(Violet-making),依此类推。
牛顿强调,这些名称来自于我们经验中的颜色。光线本身是没有颜色的,正如我们在白色的布料上染色一样。他在这段话中省略了“靛蓝”——或许对牛顿而言,“靛蓝”不是一个自然而然会用到的颜色词,又或许“制造靛蓝的”(Indigo-making)听起来像一个染色过程,具体原因我无法确定。尽管如此,《光学》还是产生了巨大的影响。此后很长时间,当人们谈起颜色时,仍然经常使用牛顿所用的相同词汇。
下图是一幅由约瑟夫·冯·夫琅和费(Joseph von Fraunhofer,1787-1826)绘制的插图,展示了他通过分光镜(spectroscope)看到的太阳光谱。颜色是用德文标注的,但为了给“Indigo”腾出位置,“Blau”在图中被上移了。(图中的颜色并非他绘制的原始图片的颜色,但与他标注的线条是相符的。)
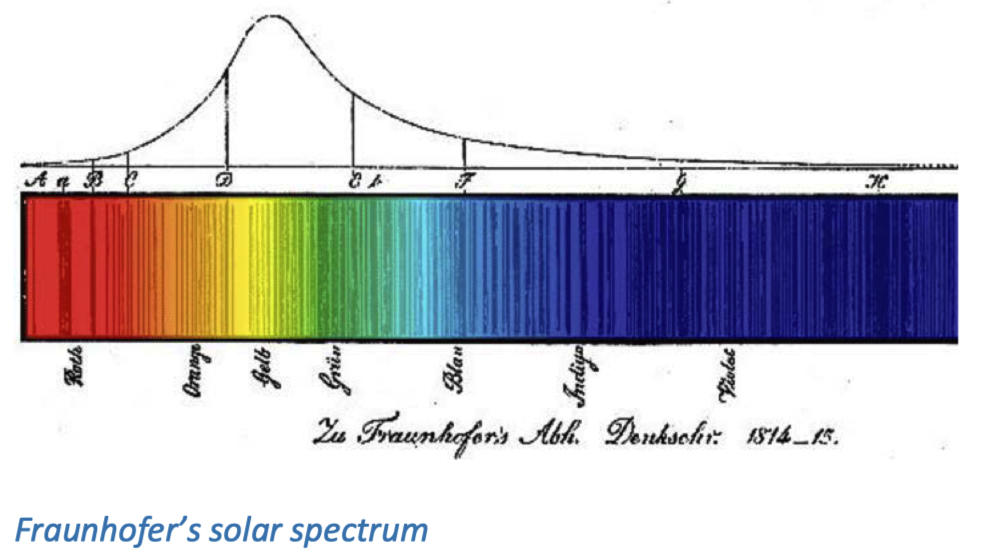
托马斯·杨采用了与牛顿相同的颜色命名方式,这并不让人意外。但我们如今已经不再习惯以这种方式来命名颜色了。所以,从现在开始,我将用“天蓝色(azure)”来指代 500 纳米附近的颜色,用“蓝色(blue)”表示 470 纳米附近的颜色。
在讨论颜色命名时,还有一个问题比较大的颜色名称。我发现有些人对“紫色(violet)”这一术语持有异议。非洲紫罗兰(African Violet)的颜色深邃浓烈,欧洲紫罗兰(European Violet)的颜色则偏向粉色。还有龙胆紫(Gentian Violet),这是一种具有抗真菌性质的人造染料,其颜色更接近于我在短波长看到的紫色。从现在开始,我打算只用“紫色(violet)”表示短波长的颜色:后续我们还将介绍紫红色(purple)、淡紫色(mauve)、品红色(magenta)和粉色(pink)。在与植物学家或园丁谈论颜色时,要格外注意这些区别。
回到托马斯·杨的测量结果。约翰·莫隆(J. D. Mollon)在其撰写的《颜色科学》(Elsevier 2003)的其中一章写道,托马斯·杨的测量数值看起来非常现代化。的确,如果将我的黄色波长与经过转换的托马斯·杨的数值相比较,会发现两者仅有约 2 纳米或 0.3% 的差异。
一个题外话:托马斯·杨是否真的能将这些微小的波长测量得如此精确?我认为这完全是可信的。他通过观察透镜(lens)和玻璃平面(glass flat)之间形成的“牛顿环”条纹(’Newton’s rings’ fringes)来进行测量。
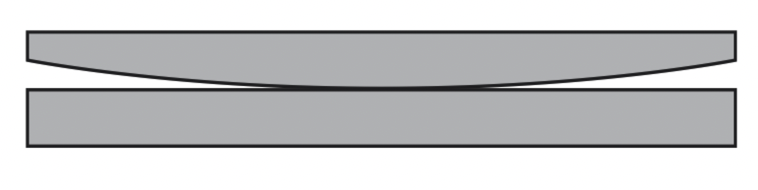
可以用两片厚玻璃圆盘制作透镜与反射镜。将其中一个圆盘安装在底座上,使其能够转动。在两个圆盘之间放上碳化硅砂磨料(carborundum grit)和水。按压、来回移动并偶尔转动上方圆盘,同时每隔一段时间转动下方圆盘。碳化硅混合物会磨削玻璃,施加的压力越强,磨掉的玻璃就越多。这就使得下方圆盘边缘磨掉了更多材质,变得凸出;上方玻璃圆盘中间磨掉了更多材质,变得凹陷。最终,这些磨砂表面(ground surface)会逐渐变成凸球面和凹球面形状,无论上方圆盘如何转动,都能够完美贴合。当表面大致成型后,就开始用更细的磨粉重复这个过程。这个湿润的表面可以用来测试形状和焦距。一旦表面达到了正确的平均形状,就使用一个可以按需流动以贴合被抛光表面的焦油抛光垫(polishing lap made of pitch),再加上红铅粉(red lead oxide),一次抛光一个表面,直至达到光学级平滑(optical flatness)。我曾在厨房的桌子上,用这种传统方法制作了一个 8 英寸、F/8 光圈的抛物面镜(parabolic mirror),其精度达到了光波长的约 1/6,效果十分出色。
制作一个光学标准平面(optical flat)要略微复杂一些。虽然可以尝试交换上下两块玻璃片的位置,但要达到让两块玻璃都不呈现凹凸状态的平衡是相当困难的。解决的关键是采用三块玻璃片,并灵活调配它们的位置。
托马斯·杨把一个透镜放在平坦的玻璃表面上,使用单色光从上方照射,并测量他看到的条纹的位置。他观察到的情形可能是这样的:

可以看到,透镜底面反射的光和玻璃平面顶部反射的光产生了干涉。两个平面接触的地方呈现暗色图案。在第一个暗条纹处,下方反射的光波移动了一个完整波长,因此在此处的干涉效果与中心相同。如果我们向外数
托马斯·杨数出了尽可能多的环状条纹,随后测量了条纹的直径。此前他已经用千分尺(micrometer)测量了球面中心与边缘的高度差,因此他能够根据条纹直径和简单的几何原理来预测这个微小空气间隙的宽度。[3]
要达到这种精度并不容易,但一定是可能的。
有多少光?
如果不想深入物理学的细节,这个故事可以简单概括如下:我们可以将光分解为不同的波长,那么有没有一种客观的方法来量化每种波长的光量呢?答案是,可以把光照在黑色的物体上,然后测量其升温情况,这可以间接告诉我们在光里包含了多少能量。
1800 年,威廉·赫歇尔(William Herschel,1738-1822)向伦敦皇家协会提交了一篇题为《棱镜色光对物体加热与照明能力的研究》的论文。他的妹妹卡洛琳·赫歇尔(Caroline Herschel,1750-1848)很可能也对这项工作有所贡献,但在那个年代不能公开告知皇家学会有女性参与了科学研究,因此他的论文全篇使用第一人称写就。我们有理由也对卡罗琳·赫歇尔的贡献表示认可,毕竟很难分辨出具体是谁做了哪些工作。
在为观测水星凌日做准备的过程中,赫歇尔通过一个直径为 9 英寸的牛顿式反射望远镜(Newtonian reflecting telescope)观察日盘。由于热量导致所有涂暗的玻璃片都裂开了,因此他开始尝试使用手头上的一些彩色滤镜。他发现,使用两个红色滤镜能够将光线减弱到可接受的水平,但他发现自己“无法忍受由于热量引起的刺激感,这表明这些玻璃并没有阻挡住热量”。
对于他感受到的刺激我并不奇怪。我曾经用一块 8 英寸的镜子做了一个简单的牛顿式望远镜,用于观测金星凌日。我没有直接观看望远镜成的像,而是把它投射到一张纸上,光孔位置大致与赫歇尔放置眼睛的地方相同。我的光孔是一块喷涂成黑色、中间开孔的木板,在阳光的照射下,它在几秒钟内就着火了。
赫歇尔并没有因此气馁,他转而尝试使用绿色玻璃片进行实验。两块绿色玻璃片不仅降低了阳光的强度,也消除了热感。他原本认为所有波段的可见光对“聚光玻璃效应(burning glass effect)”的贡献是相等的,然而红光使他的眼睛发热,但绿光却没有这种效果。为了探索光谱中哪些部分的光贡献了最多的热量,他构建了一套特殊的实验装置。
在这项独立的实验中,他利用窗边的大棱镜投射出一束光谱,落在一个带有狭缝的可调角度倾斜屏幕上。通过调整装置,可以使一条指定颜色的光带落在温度计的玻璃球上,玻璃球用印度墨水涂黑以吸收光线。借助这套装置,他就可以精确测量每分钟升温的速度了。
下图摘自他的论文(《伦敦皇家学会哲学交流录》第 90 卷(1800 年)第 262 页,经皇家学会许可转载)。
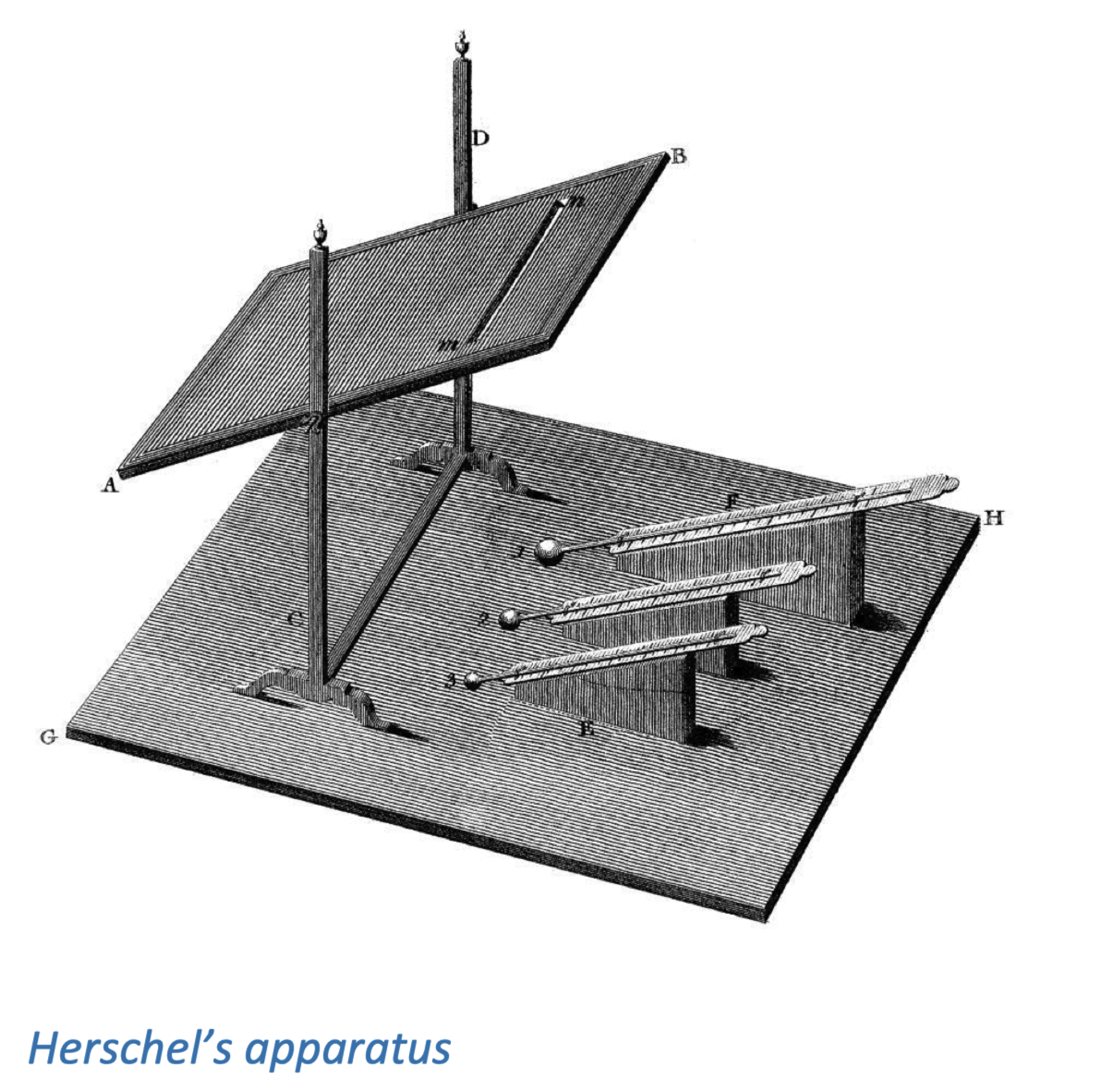
他使用了三个温度计进行实验。他自己的温度计是最大的那个,另两个是从朋友那里借的。事实证明,这两只小温度计的结果匹配得很好,因此他将其中一只放置在光带照射下,用于记录温度上升,另一只则放在阴影中,用于校正其他因素导致的温度变化。他还用自己的大温度计来验证这两只温度计的读数。他发现,红光产生的热量是绿光的两倍多,是紫光的三倍半。事实上,产生热量的峰值似乎位于可见红光之外的红外线区域。
随后,他用显微镜取代温度计,观察了硬币、彩纸和钉子等对象,并记录在不同色光下能分辨出多少细节。他发现他分辨细节的能力(ability to resolve detail)在黄绿色光线的照射下达到了顶峰,而在紫色光线的照射下则特别差。这种不太引人注目的黄绿色,其波长近似于我们之前提到的国际单位“坎德拉”定义中使用的 555 纳米的光亮度(luminance)。
把光转化为热来测量确实是个好主意。物理学家伦福德伯爵(Count von Rumford,1753-1814)在上述实验两年前就曾指出,机械功(mechanical work)——在他的例子里是大炮筒的加工——可能与产生的热量有关。在这篇论文中,威廉·赫歇尔差一点就将温度上升与吸收的辐射量直接联系起来了。他谨慎地考虑到,他所观察到的光和测量的温度上升可能是两种完全不同的辐射形态,只是碰巧被棱镜以类似的方式分散开了。然而,赫歇尔兄妹观察到,我们分辨细节的能力随着颜色的变化而变化;我们看到的颜色是更大的光谱的一部分;可以通过将辐射转换为黑化物体(blackened body)的升温值,间接测量辐射量。对于可能只用了一下午时间进行的初步实验来说,能得到这些结论已经很不错了。
在接下来的一年(1801 年),约翰·威廉·里特(Johann Wilhelm Ritter,1776-1810)受赫歇尔实验的启发,发现了另一种形式的不可见辐射——紫外线。众所周知,氯化银在阳光照射下会变黑,这成为了后来摄影术的基础,但当时还没有办法把图像“固定”下来。里特尝试了不同光谱颜色对氯化银变黑效果的影响。这次,红光几乎起不到作用,但从紫色到紫外线的波段,会使变黑程度逐渐增强。
赫歇尔最初的实验是开创性的,但其实验装置的准确性有限。他只测量了光谱中的红色、绿色、蓝色三个波段,并且假设太阳光的亮度(brightness)不会有明显变化。他尝试使用更小的狭缝来单独测量黄色,但未能获得足够的光量来产生可以测出的温度变化。在接下来几年中,赫歇尔和其他许多科学家提升了探测器的灵敏度,他们用热电偶(thermocouples)等需要更少光照即可升温的更小型探测器取代了温度计。
1878 年,S. P. 兰利(S. P. Langley)制造了第一台测辐射热计(bolometer)[4]。这种仪器的工作原理与赫歇尔使用的黑化温度计相似,但它是通过测量一块黑化的铂金片因温度升高导致的电阻变化来量化光的强度。当铂金片的温度升高时,其电阻值就会上升。使用铂金片作为探测器是一个很好的选择:它可以做得很纯、很薄,而且不会氧化。纯净材料的电阻变化与绝对温度大致成线性关系。在现代,最灵敏的测辐射热计会被冷却到接近绝对零度,以提高灵敏度。但在当时没办法将装置冷却到如此低温,因此他们考虑在绝对温度约为 300 开尔文(26.85 摄氏度)的基础上寻求 1 度的温度升高。虽然这种方式听起来效果可能不太明显,但可以把铂金片加工至极薄,使其在吸收相同能量时升温更多。在海底电报领域的其他电气测量方面,汤普森的电流计(galvanometer)和惠斯通电桥(Wheatstone’s bridge)[5] 也对这一进展做出了重要贡献。下面是一张约 1880 年用于摩尔斯电报长途传输的电流计的图片。
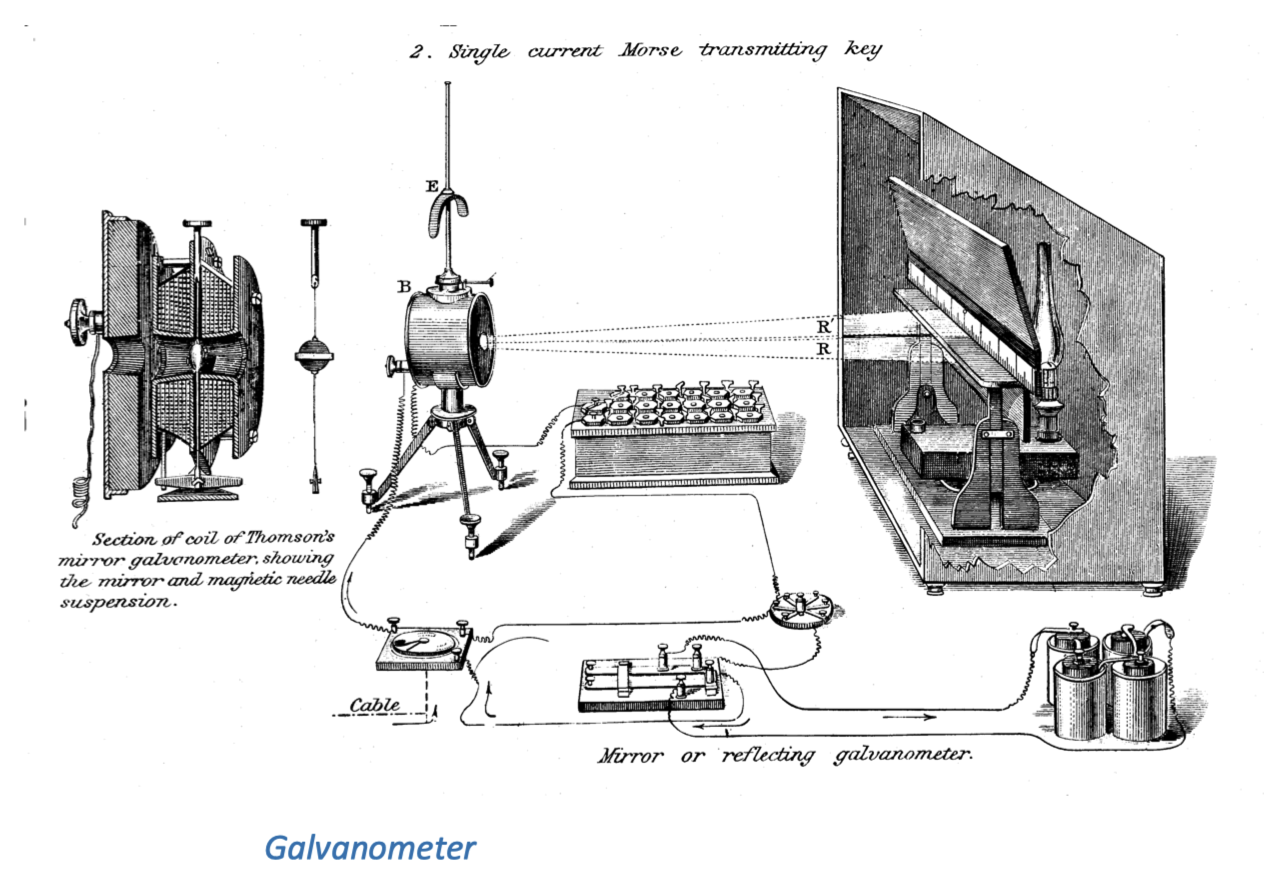
在那个时代还没有现成的电流放大器(amplifier),横跨大西洋的电缆是一根很长的电线,需要做大量的工作才能检测出到电线远端的微小电信号。在图中,电流通过线圈产生磁场,线圈中间放置了一个略微凹陷的小镜子,镜子背面附有一根条形磁铁,悬挂在一根单丝纤维上。当电流流过时,磁场对条形磁铁产生扭矩(torque),导致磁铁和镜子转动,直到电磁力与纤维的扭力(torsion)达到平衡。由于这种扭力非常小,即使是微小电流也可以产生显著的偏转。整套装置都放在一个密封罐中,隔绝了空气流动、温度、湿度变化的影响。装置的光源设计为一个带竖线的圆点,当其光线聚焦在镜子上反射出来,并投射到标尺上时,会形成一个带有中心暗线的聚焦圆点。这就相当于一个更轻、更长的传统电流表(ammeter)指向臂。如果使用惠斯通电桥进行电压比较,就可以在建立连接时,通过光点的摆动方向检测到微小的电压差异。随后可以用一个电阻将线圈短路以减缓摆动,为下次测量做准备。
后来发明的电流计(galvanometer)采用了石英纤维(quartz fibres)技术。其中最优质的石英纤维是由查尔斯·弗农·波伊斯爵士(C. V. Boys,1855-1944)开发的一种独特的工艺制成的:将一根石英棒加热至发出黄光,然后将一端固定夹紧,另一端连接到一个螺栓上,将螺栓使用强力弩(crossbow)射入真空管中,从而产生了极细、强度极高的纤维,在张力作用下也不会产生扭曲 [6]。得益于这些技术突破,到 1880 年代就已经能够测量低至十亿分之一安培的恒定电流了。兰利甚至声称,后来的仪器能够探测到四分之一英里外的一头牛产生的热量。我喜欢这个用一头“参考牛”来校准探测器的想法,但是否有过实际测试就不得而知了。这种探测器后来被用于测量透过一块大型岩盐棱镜(prism of rock salt)观测到的恒星光谱中的微小细节,所以它能探测到一头牛的热量是完全有可能的。
我曾用类似的仪器做过实验,只是缺少了牛这一环节。在当下,你可能不需要亲自动手这样做了:市面上的现代测辐射热计可能是一种紧凑的手持设备,配备了数字显示屏,能够轻松帮你完成复杂的测量工作。然而,如果你亲手用类似原始仪器的设备进行测量,就能欣赏到其设计的优雅之处。
测辐射热计在当前的研究中仍在使用。它们作为一种标准仪器,能让我们以标准单位准确测量任何波长的辐射量。它们不是特别敏感,但在远红外区域,它们的敏感度可以和任何其他设备媲美。在可见光谱范围内,测辐射热计经常用于校准其他更敏感的设备,如硅探测器(silicon detectors)。而在远红外成像技术中,现代相机可能会使用一系列测辐射热计组成的阵列。
分光镜(spectroscope)
我们之前看到了夫琅和费对太阳光谱的描绘。约瑟夫·冯·夫琅和费在贝内迪克特博依恩光学研究所(Benediktbeuern Optical Institute)担任研究主管和主任,负责开发和改进玻璃制造工艺,以及研制新的玻璃配方。玻璃独特的色散性质——即折射率随波长发生变化,也是导致棱镜产生彩虹的原因——在制造透镜时是个麻烦,会导致不同波长的光聚焦于不同位置,从而产生色差(chromatic aberration)。解决这种色差的方法是将凸透镜和凹透镜粘合在一起,制成消色差双合透镜(achromatic doublet)。这两片透镜由不同类型的玻璃制成,通过精心选择玻璃,可以使一片透镜的色差抵消另一片透镜的色差。在夫琅和费之前,制作消色差双合透镜的专家都在伦敦工作(特别是 1750 年成立的多隆德和艾奇森(Dollond and Aitchison)公司,其在 2009 年被博特斯眼镜店(Boots Opticians)收购时才失去了多隆德的名字)。夫琅和费的目标是把巴伐利亚建设成优秀的消色差双合透镜生产中心,这意味着他必须生产出非常精确和均匀的棱镜,并尽可能准确地测量它们的色散特性。
夫琅和费需要一组特定的光谱颜色来进行测量。仅仅像牛顿那样用肉眼将光分成七种颜色是不够的,他需要一种精确地分割光谱的方法。沃拉斯顿(William Hyde Wollaston,1766-1828)在 1802 年指出,太阳光中存在七条暗线。在 1813 年或 1814 年,夫琅和费自己建造了一个分光镜(spectroscope)。他在窗户的叶片上开了一个狭缝,使用一块 60 度角的火石玻璃棱镜(flint glass prism)和一个小型望远镜来观察光谱,所有设备都安装在一个用墨水涂黑的旧雪茄盒子里。结果,他看到的不仅仅是七条线,而是数以百计的暗线和细微线条。他给最明显的十条线条标上了字母,并使用更精密的仪器测量了约 350 条线的精确角度。这些线条自此以后就被称为夫琅和费线(the Fraunhofer lines)[7]。通过这些线条,他就能在不同材料制成的棱镜中找到相同的线条,并利用结果设计出一款消色差双合透镜。
夫琅和费在设计消色差透镜时并不需要直接用到光的波长信息,但他肯定希望基于绝对数值测量的方法来研究光谱,而不愿意只依赖于适应他手头玻璃材料的任意公式。为了测量波长,他用衍射光栅(diffraction grating)[8] 替换了分光镜中的棱镜。他最初巧妙地用细铁丝缠绕在细螺纹上制成了衍射光栅,光栅条纹的间距与光的波长共同决定了光的偏转角度,因此通过测量偏转角度就可以知道光的波长。由此可见,光栅的工作原理有点像棱镜,但它能够为光谱中的每个波长提供一个完全可预测的、精确的角度偏移。
我之前提到,赫歇尔观察到的黄绿色可能对应 555 纳米波长的峰值光亮度(peak luminance)。他发现人眼在黄绿色的光线下对细节的辨识能力最强,但这种现象可能只适用于他选择的特定棱镜。如果换一个棱镜,可能会拉长绿色和黄色的光谱,而压缩橙色和红色的光谱,导致黄绿色看起来更暗,而橙红色看起来更亮。不过在实际应用中,大多数透明玻璃都能够相对均匀地分散光谱,因此赫歇尔观察到的黄绿色可能接近于 555 纳米的峰值光亮度。有些特殊类型的玻璃在分散光谱时非常不均匀,有些甚至可以将光谱折叠回自身,但这些玻璃都是深色的,不适用于制造透镜或棱镜。
我们之前探讨了托马斯·杨如何使用他的简单装置精确测量光的波长,尽管他还需要其他设备来辅助将光分散成不同的波长。那么,夫琅和费的光栅是如何同时做到分光、测光这两件事的呢?
夫琅和费制作了十个光栅,并针对每个光栅的 D 线 [9] 测量了多个不同的“阶次”。通过汇总这些测量结果,他得出了 D 线的平均波长值为 588.8 纳米。
夫琅和费观察到的被称为吸收 D 线(absorption D-line)的现象,实际上源自钠元素的两条光谱线,不过当时人们还未将其与钠元素直接联系起来。根据现代科学的测量,这对钠双线的波长分别是 588.9950 纳米(较亮的线)和 589.5924 纳米(较暗的线)。如果将较亮的线的波长除以 1.00027(空气折射率的良好平均值),我们可以得到一个接近实际条件的波长,即 588.83 纳米。夫琅和费在这方面的工作非常精细,但也不得不仰仗一些运气,因为即便在那个时代,米的定义也没有现在这样精确。
到 1823 年,夫琅和费制造出了一些更精细的光栅,玻璃板上刻线的密度最高达到每毫米 300 条。他使用这些光栅来测量太阳、恒星和行星的光谱。制作光栅的刻线技术在 19 世纪得到了持续的发展和完善。
光谱仪(spectrometer)
如果把夫琅和费的分光镜和兰利的测辐射热计结合起来,就得到了一种称为光谱仪(spectrometer)的仪器。这种仪器能够精确测量光在各个波长上的强度,并用标准的科学单位来表示。现代的光谱仪使用一组探测器阵列,能够同时测量所有波长。虽然它可能不会直接使用测辐射热计阵列来测量可见光,但可以采用基于其他标准的测辐射热计来进行校准。
如果将光谱仪对准一个红色物体进行测量,会得到一组数字,显示在 400 纳米一端的光强度较低,而 700 纳米一端的值光强度较高。这个结果符合我们对红色物体的期待,但它并没有告诉我们关于实际颜色感知的信息。
广谱峰值(broad spectrum peaks)
在光谱分析中,通常由波长(以纳米为单位)定义光谱带,并用瓦特(功率)或焦耳(= 瓦特×秒)来测量每个光谱带的光量,这种做法已经相当标准化。然而,当我们翻阅科学论文,尤其是那些历史文献时,有时会发现科学家们使用频率(而非波长)来描述光谱带,并且以光子数(或每秒光子数)来衡量光量。
这种差异重要吗?
单位“坎德拉”就是基于人眼在 555 纳米波长附近感知到的峰值敏感度(peak sensitivity)定义的。敏感度衡量的是在每增加一个单位的光量时,人眼所获得的“刺激”(stimulus)的强度。我们将在下一章中讨论“刺激”是什么,在这里先假设它是光的“视亮度”(how ‘’bright‘’ the light looks)。敏感度通常按峰值为 1.0 来缩放,这也是我们在这里要做的。如果人眼对一个波段的敏感度为 0.5,意味着我们需要两倍的光量才能感知到相同的视亮度(brightness)。如果一个波段的敏感度为零,则表明我们的眼睛无法看到这种光。
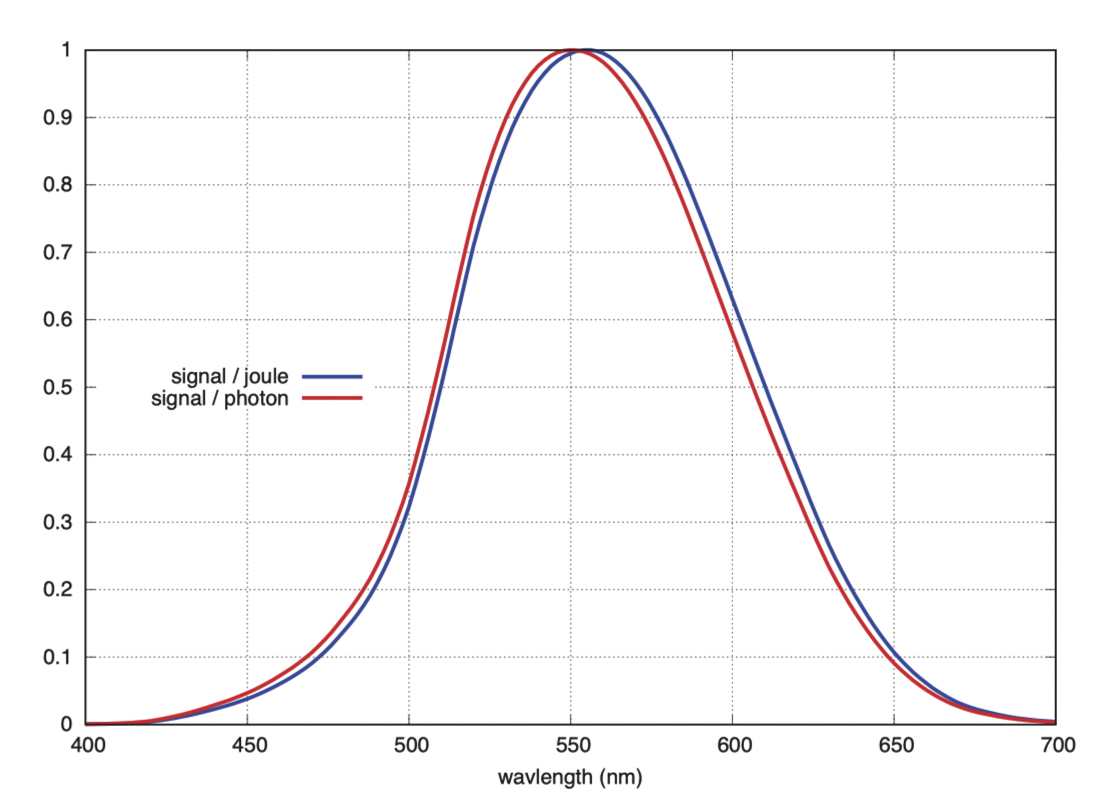
在这里,我们通过一个图表展示了人眼对可见光谱的敏感度变化。
图中的蓝色曲线根据波长(纳米)来定义光谱带,其敏感度是以基于焦耳单位的曝光量来计算的。蓝色曲线的敏感度峰值在 555 纳米处。在下一章讨论视亮度(brightness)单位时,我们会再次回顾这条曲线。
红色曲线虽然也按波长(纳米)定义,但其敏感度是根据以光子数计量的曝光量来计算的。由于短波长光子具有更高的能量(参见本章开头的表格),每焦耳能量含有的光子数就会较少,导致红色曲线的敏感度峰值位于 550 纳米处。虽然 550 纳米与 555 纳米之间只有 5 纳米的差异,但足以让我们看出在这两个波长下光的视觉感知差别。如果我们改用频率而非波长作为图表的横轴,则敏感度的峰值还会再次移动。这表明,敏感度峰值的确定在很大程度上取决于我们如何展示数据。
无需过分担忧这些差异。就像我们讨论空气中和真空中波长的差异一样,我现在提及这些内容,只是为了避免未来的混淆。但在实际应用中,这种差异通常不会造成问题。
反射和透射光谱
一种颜色的反射光谱,指的是在各个波长下,有多少光被这种颜色反射出来。为了准确测量这个比例,我们需要将观察到的颜色光谱与相同照明下理想的漫反射白(diffuse white)标准物的光谱相除。我手头没有理想的漫反射白标准物,但我有一块硫化钡(barium sulphide)瓷砖,它在所有波长下的反射率介于 95 % 到 98 %之间,并且进行过反射率校准。选择这种材料比选择普通的含有荧光增白剂的白纸更为科学可靠。此外,进行这类测量还需要一个良好的光源,能够发出覆盖所有波长、分布均匀的光谱。
以下是孟塞尔颜色图册(Munsell Colour Atlas)中选取的几种色卡的反射率测量值。
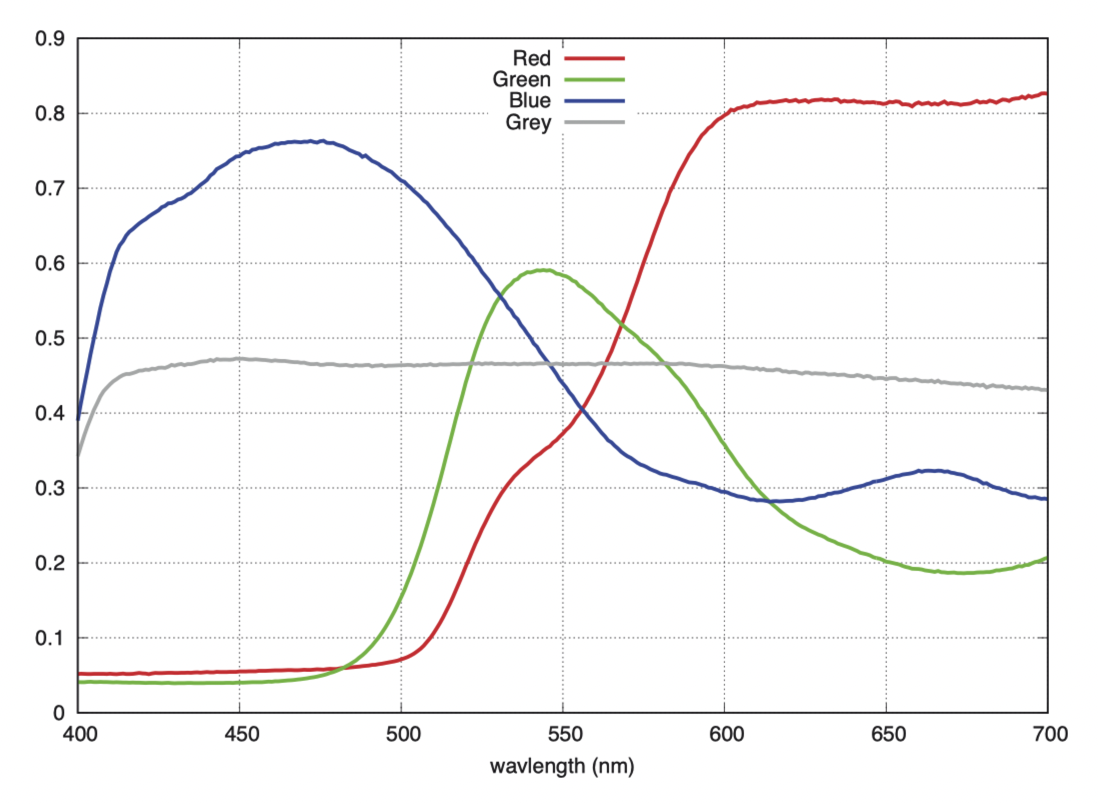
反射率(reflectance)的数值应该在 0 到 1 之间。这些颜色的孟塞尔值都相同。绿色和蓝色色卡的反射率峰值不到 50%,而红色色卡的反射率峰值则超过 70%,这样的反射率分布在颜色科学中是很常见的。
有很多机制可以使染料和颜料吸收高于某个能量水平的光子。镉黄(Cadmium Yellow, CdS)是一种带隙(band gap)为 2.4 eV 的半导体,会吸收超过 2.4 eV 能量的光子(参见本章开头表格),因此呈现出明亮的黄色。同理,朱砂(HgS)也是一种带隙较小(2.0 eV)的半导体,因此呈现出明亮的红色。简而言之,有许多明亮的颜料和染料吸收短波长的光,反射或透射长波长的光,从而呈现出鲜艳的颜色。相对地,吸收长波长或中波长光的材料比较少,这些材料通常反射性不强,颜色也不那么鲜亮。值得注意的是,绿色峰值在短波长端的斜率更陡峭,这可能意味着其颜色效果是由两种不同的通带滤波器(passband filters)共同作用的结果。更多关于这方面的内容,请参阅库尔特·纳萨乌(Kurt Nassau)的著作《颜色的物理与化学》(The Physics and Chemistry of Colour)。
灰色的测量结果几乎是一条平坦的直线。这种均匀反射的特性,是通过将反射能力极强的白色和吸光能力极强的黑色以适当比例混合而得到的。
透射光谱(transmission spectrum)的测量与反射光谱相似,但测量的是透过待测物体的光。在测量透射光谱时,不需要白色的参照物(reference white),因为未被任何物体阻挡的光源本身就是我们的参照标准。如果测试物体是不透明或乳白色的,则对其光谱特性的分析会变得更加复杂。更多信息请参见第 10 章。
- 1.Dover Books 是一家美国图书出版商,由 Hayward Cirker 和他的妻子 Blanche 于 1941 年创立,主要重新发行原始出版商已绝版的书籍。这些通常(但不总是)属于公共领域的书籍,其最初出版的版本十分稀少,具有历史意义。Dover 重新出版了这些书籍,使获得它们的成本显着降低。Dover 重印了 18 和 19 世纪的经典文学作品、古典乐谱和公共领域的图像,还出版了大量数学、科学和工程文本。 ↩
- 2.光程(light path)是光学领域的一个基础概念,常用
表示,其定义为光传播的几何路程 与所在介质折射率 的乘积, 。光程差(light path difference)为两束光光程的差值。 ↩ - 3.等厚干涉-牛顿环曲率半径测量 大学物理实验——干涉法测微小量(牛顿环) ↩
- 4.测辐射热计是用于检测微小辐射能量的仪器,可测量可见光、红外线、激光或微波的辐射能。若将它装在火箭或高空气球上,可避开大气的影响,进行天文观测。在电子学中,用它可测量微波源的输出功率。通常的测辐射热计是由惠斯通电桥构成,电桥的二个臂是二条相同的薄铂条。当某一铂条被很弱的(小于10-13焦耳)辐射所照射时,它的电阻会发生微小的变化,则可通过测量电阻的变化来估算辐射能。另一种测辐射热计是由一片粘在石英板上的半导体膜构成的光敏元件来代替桥臂上的铂条。此外,还有一种超导测辐射热计,它利用了某种薄膜(例如硝酸铌)在温度4K左右时,在电导率由正常态向超导态过渡的过渡点附近其电阻随温度急剧变化的性能。这种测辐射热计灵敏度很高,可用以精密测量很弱的辐射如红外辐射和激光的功率。 ↩
- 5.惠斯通电桥(又称单臂电桥)是一种可以精确测量电阻的仪器,于1833年由塞缪尔·亨特·克里斯蒂发明,1843年由查尔斯·惠斯通改进及推广。它用来精确测量未知电阻器的电阻,原理与原始的电势差计相近。 ↩
- 6.光纤历史与波伊斯石弓实验 ↩
- 7.夫琅和费线(Fraunhofer lines,港台译作夫朗和斐谱线)是一系列以德国物理学家约瑟夫·夫琅和费(1787年─1826年)为名的光谱线,这些是最初被当成太阳光谱中的暗特征谱线。英国的化学家威廉·海德·沃拉斯顿是在1802年第一位注意到有一定数量的黑暗特征谱线出现在太阳光谱中,夫琅和费独立地再度发现这些谱线,并且开始系统性的研究与测量这些谱线。最后,他绘出了570条的谱线,并且以字母A到K标示出主要的特征谱线,较弱的则以其他的字母标示。后来古斯塔夫·基尔霍夫和罗伯特·本生确认了每一条谱线所对应的化学元素,并推论在太阳光谱中的暗线是由在太阳上层的那些元素吸收造成的,有些被观察到的特征谱线则是地球大气层中的氧分子造成的。由于夫琅和费线的波长都已经明确地被定义,所以常被用作说明光学材料的折射率和色散特性。夫琅和费线也是著名的吸收谱线,因而整个太阳吸收光谱常被称为“夫琅和费光谱”(夫琅和费光谱)。 ↩
- 8.衍射光栅通过有规律的结构,使入射光的振幅或相位(或两者同时)受到周期性空间调制,其在光学上的最重要应用是作为分光器件,常被用于单色仪和光谱仪上。衍射光栅通常是在表面上有沟槽或刻痕的平板,其通常所讲的衍射光栅是基于夫琅和费多缝衍射效应工作的。描述光栅结构与光的入射角和衍射角之间关系的公式叫“光栅方程”。 ↩
- 9.D-lines:在光谱学领域,D线指的是钠元素在光谱黄色区域的一对特征线条。这两条线条之间的距离非常细微,以至于仅用分辨率较低的光谱仪是难以区分的。这条线是从红色端开始计的太阳光谱中的第四个显著吸收线,因此被赋予了“D”这一字母标识。经过进一步的研究,D线被细分为D1和D2两个组成部分,它们的波长分别是5895.924埃和5889.950埃(1埃等于10^-10米)。此外,还发现了一个由氦元素引起的、位于色球中的发射线D3,其波长为5875.62埃。 ↩
转载请注明来源。欢迎留言评论,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。